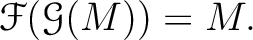Next: About this document ...
体 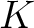 のガロア拡大
のガロア拡大 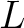 が与えられているとする。
が与えられているとする。
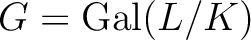 の部分群
の部分群 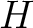 に対して、
に対して、
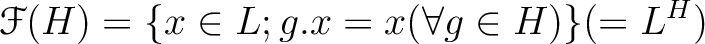
 と
と 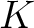 の中間体
の中間体 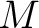 に対して、
に対して、
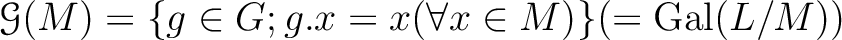
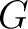 の任意の部分群
の任意の部分群 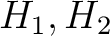 に対して、
に対して、
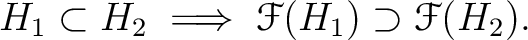
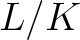 の任意の中間体
の任意の中間体 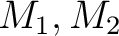 に対して、
に対して、
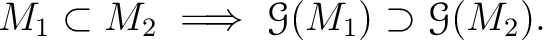
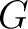 の任意の部分群
の任意の部分群 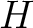 にたいして、
にたいして、
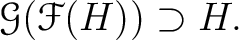
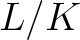 の任意の中間体
の任意の中間体 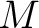 に対して、
に対して、
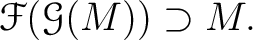
実は、上の (1)-(4) から、全く形式的な計算で次のことが成り立つことがわかる。
("3回=1回")
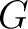 の任意の部分群
の任意の部分群 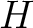 にたいして、
にたいして、
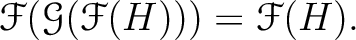
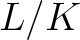 の任意の中間体
の任意の中間体 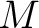 に対して、
に対して、
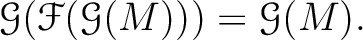
ガロア理論では、さらに次のことが分かる。(狭義単調減少性)
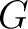 の任意の部分群
の任意の部分群 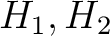 に対して、
に対して、
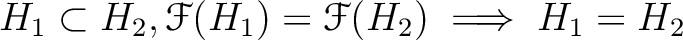
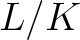 の任意の中間体
の任意の中間体 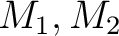 に対して、
に対して、
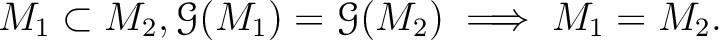
このことから、最後に次のことが分かる。
("2回=0回")
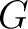 の任意の部分群
の任意の部分群 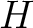 にたいして、
にたいして、
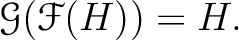
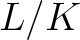 の任意の中間体
の任意の中間体 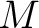 に対して、
に対して、