Next: About this document ...
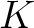 に対して
に対して 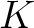 を含む代数的閉体が存在する。
を含む代数的閉体が存在する。
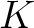 に対して
に対して 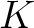 を含む代数的閉体が存在する。
を含む代数的閉体が存在する。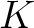 上の 既約一変数モニック多項式をすべて考え、それらを
上の 既約一変数モニック多項式をすべて考え、それらを
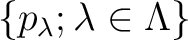
 のそれぞれに対して変数
のそれぞれに対して変数 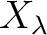 を
一つづつ取り、無限変数の多項式環
を
一つづつ取り、無限変数の多項式環
![$R=K[\{X_\lambda; \lambda \in \Lambda\}]$](img6.png) を考えよう。
を考えよう。
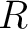 の元とは、
の元とは、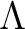 から有限個
から有限個
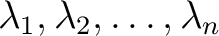 をとって、それらの変数の多項式、
すなわち
をとって、それらの変数の多項式、
すなわち
![$K[X_{\lambda_1},\dots, X_{\lambda_n}]$](img10.png) の元を考えたものである。別の言い方をすると:
の元を考えたものである。別の言い方をすると:
![$\displaystyle R=K[\{X_\lambda; \lambda \in \Lambda\}]=
\bigcup_{n=1}^\infty
\le...
...n \in \Lambda}
K[
X_{\lambda_1},
X_{\lambda_2},
\dots ,X_{\lambda_n}]
\right)
$](img11.png)
多項式環の現代的な定義は、 「代入原理を満たす環のうち普遍的なもの」という形で 与えられる。
さて、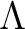 の各元
の各元 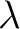 に対して、
に対して、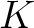 上の一変数多項式が
対応するわけだから、これを
上の一変数多項式が
対応するわけだから、これを
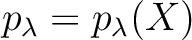 とおく。
とおく。
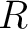 のイデアル
のイデアル 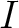 を
を
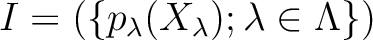
主張1:  .
.
 とすると、
とすると、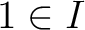 , すなわち、ある
, すなわち、ある
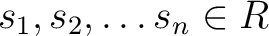 と
有限個の
と
有限個の
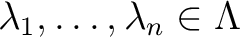 が存在して、
が存在して、
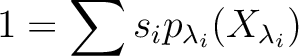
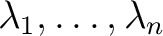 を
を
 , その他
, その他 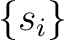 に
出てくる変数を全部で
に
出てくる変数を全部で
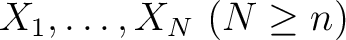 と書くと、
と書くと、
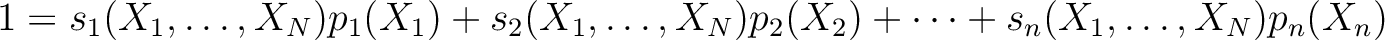 |
(あ) |
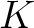 の有限次拡大体
の有限次拡大体 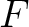 で、
で、
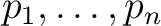 の
根
の
根
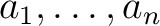 をすべて含むもの
(積
をすべて含むもの
(積
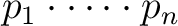 の分解体:命題4.2参照)を取れば、
(あ)はもちろん
の分解体:命題4.2参照)を取れば、
(あ)はもちろん  上の
多項式としても成立している。(あ)の両辺に
上の
多項式としても成立している。(あ)の両辺に
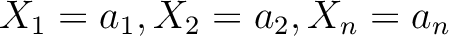 を代入すると、
を代入すると、 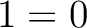 となって矛盾を得る
となって矛盾を得る
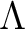
主張 1 と Zorn の補題により、
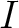 を含む
を含む 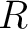 の極大イデアル
の極大イデアル
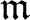 が存在することがわかる。
そこで、
が存在することがわかる。
そこで、
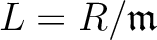
| [ |
|---|
l](※)
|
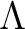 の定義により、
の定義により、
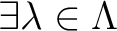 が存在して、
が存在して、
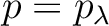 がなりたつ。
がなりたつ。
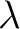 に対応する変数
に対応する変数 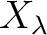 に対し、
に対し、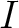 の定義により
の定義により
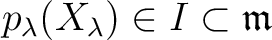
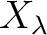 の
の 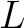 でのクラスを
でのクラスを 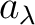 と書けば
と書けば
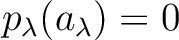 である。
である。
さて、実は次の主張が成り立つ。これを用いれば定理0.1の証明が終了する。
| [ |
|---|
l]主張2
(※)を満たす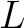 が与えられているとする。このとき、 が与えられているとする。このとき、
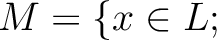 $x$ は $K$ 上代数的 $x$ は $K$ 上代数的
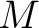 は は 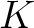 を含む代数閉体である。 を含む代数閉体である。
|
が、主張2の証明は難しい上に、本講義のまだ証明していない結果を多数用いるので、 この時点でこれを用いるのは適当ではない。
そこで、主張2の代わりに 次のような間に合せの議論でさしあたって満足しておくことにする。
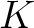 にたいして、先程の議論で
にたいして、先程の議論で 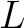 という体を作ることができた。
これを
という体を作ることができた。
これを 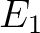 と呼び替えることとする。
と呼び替えることとする。
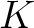 上の一変数多項式は必ず
上の一変数多項式は必ず 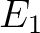 に一つの根を持つ。
に一つの根を持つ。 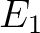 に同様の操作を行うことにより、
に同様の操作を行うことにより、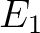 の
拡大体
の
拡大体 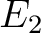 を作ることができる。
を作ることができる。
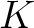 上の一変数多項式は必ず
上の一変数多項式は必ず 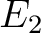 に一つの根を持つ。
これを繰り返して
に一つの根を持つ。
これを繰り返して
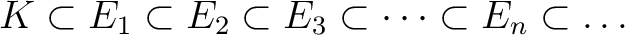
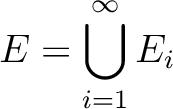
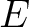 は
は 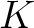 の拡大体であって、
の拡大体であって、
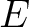 上の一変数多項式は必ず
上の一変数多項式は必ず 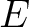 内に根を持つ。
すなわち、
内に根を持つ。
すなわち、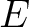 は代数的閉体である。
は代数的閉体である。
主張2 の証明についてはまた気の向いたときに行うことにする。
この稿の作成に当たっては永田「可換体論」を用い...て済ますつもりであったが (「かわりに」以降の部分で)S. Lang の algebra も参考にした。証明全体のアイディアは E. Artin によるものと 聞く。