Next: About this document ...
Yoshifumi Tsuchimoto
In this lecture we make use of a
scheme ![]() of finite type over
of finite type over
![]() ,
It is a patchwork of
affine schemes of finite type over
,
It is a patchwork of
affine schemes of finite type over
![]() ,
,
An affine scheme ![]() of finite type over
of finite type over
![]() , in turn, is related to a
set
, in turn, is related to a
set
![]() of polynomial equations of coefficients in
of polynomial equations of coefficients in
![]() ,
and is written as
,
and is written as
![]() for a ring
for a ring
![]() of finite type over
of finite type over
![]() ,
We consider quasi coherent sheaves over these objects. When
,
We consider quasi coherent sheaves over these objects. When ![]() is
affine (
is
affine (
![]() ), the category of quasi coherent sheaves over
), the category of quasi coherent sheaves over ![]() is equivalent to the category of
is equivalent to the category of ![]() -modules.
-modules.
For any scheme ![]() of finite type over
of finite type over
![]() , we put
, we put
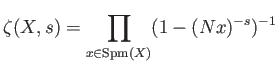
Recall we have defined the congruent zeta function as
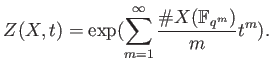
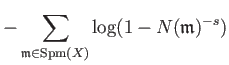 | ||
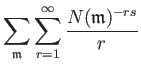 | ||
![% latex2html id marker 792
$\displaystyle \sum_{u=1}^\infty \sum_ {\substack{\m...
...hfrak{m} : \mathbb{F}_q]=u}} \sum_{r=1}^\infty \frac{N(\mathfrak{m})^{-rs} }{r}$](img17.png) | ||
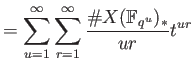 |
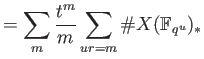 | |
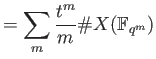 | ||
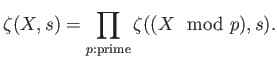 |