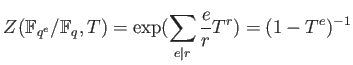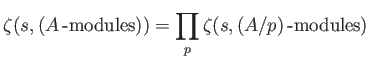DEFINITION 6.1
Let
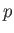
be an odd prime. Let
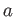
be an integer which is not divisible by
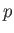
.
Then we define the
Legendre symbol
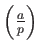
by
the following formula.
We further define
LEMMA 6.2
Let 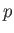 be an odd prime. Then:
be an odd prime. Then:
-
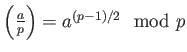
-
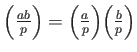
We note in particular that
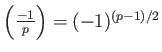 .
.
DEFINITION 6.3
Let
be distinct odd primes.
Let
be a primitive
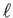
-th root
of unity in an extension field of
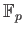
.
Then for any integer
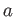
, we define a
Gauss sum 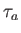
as
follows.
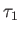
is simply denoted as
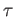
.
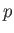 -dependence of zeta functions is important topic.
We are not going to talk about that in too much detail but
let us explain a little bit.
-dependence of zeta functions is important topic.
We are not going to talk about that in too much detail but
let us explain a little bit.
Let us define
the zeta function of a category
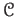 [1].
[1].
where 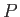 runs over all finite simple objects.
runs over all finite simple objects.
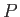 : finite
: finite
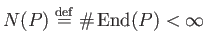 .
.
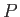 : simple
: simple
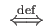
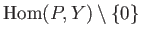 consists of mono morphisms.
consists of mono morphisms.
For any commutative ring 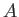 ,
an
,
an 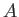 -module
-module 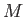 is simple if and only if
is simple if and only if
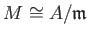 for some maximal idea
for some maximal idea
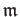 of
of 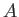 . We have thus:
. We have thus:
Let us take a look at the last line.
It sais that the zeta is a product of zeta's on 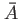 .
Let us fix a prime number
.
Let us fix a prime number 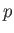 , put
, put
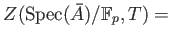 , and concentrate on
, and concentrate on 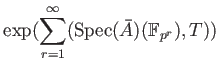 to go on further.
to go on further.
We conclude:
PROPOSITION 6.6
Let 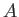 be a commutative ring. Then:
be a commutative ring. Then:
- We have a product formula.
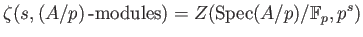 is obtained by substituting in the
congruent zeta function by .
is obtained by substituting in the
congruent zeta function by .
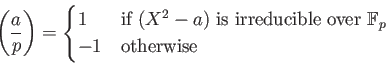
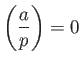
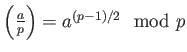
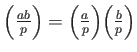
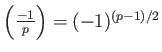 .
.
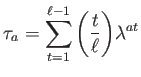
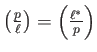 (
where
(
where
![]() [1].
[1].
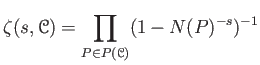
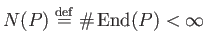 .
.
![]() ,
an
,
an ![]() -module
-module ![]() is simple if and only if
is simple if and only if
![]() for some maximal idea
for some maximal idea
![]() of
of ![]() . We have thus:
. We have thus:
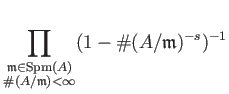
![$\displaystyle \prod_{p:\text{prime}} \prod_ {\substack{\mathfrak{m} \in \operat...
...[A/\mathfrak{m}: \mathbb{F}_p]<\infty }} (1-\char93 (A/\mathfrak{m})^{-s})^{-1}$](img41.png)
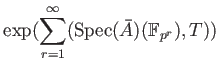 to go on further.
to go on further.
![$\displaystyle \zeta(s,(A/p)\operatorname{-modules}) = \prod_ {\substack{\mathfr...
...athfrak{m}: \mathbb{F}_p]<\infty }} (1-\char93 (\bar A/\mathfrak{m})^{-s})^{-1}$](img47.png)