Congruent zeta functions. No.3
Yoshifumi Tsuchimoto
DEFINITION 3.1
Let
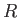
be a ring. A polynomial
![$ f(X_0,X_1,\dots,X_n)\in R[X_0,X_1,\dots, X_n]$](img3.png)
is said to be
homogenius of degree
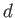
if an equality
holds as a polynomial in
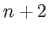
variables
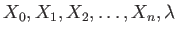
.
For any homogeneous polynomial
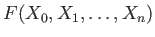 , we may
obtain its inhomogenization as follows:
, we may
obtain its inhomogenization as follows:
Conversely, for any inhomogeneous polynomial
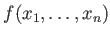 of degree
of degree 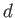 ,
we may
obtain its homogenization as follows:
,
we may
obtain its homogenization as follows:
DEFINITION 3.2
Let
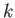
be a field.
- We put
and call it (the set of 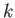 -valued points of) the projective space.
The class of an element
-valued points of) the projective space.
The class of an element
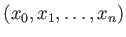 in
in 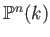 is
denoted by
is
denoted by
![$ [x_0:x_1:\dots:x_n]$](img16.png) .
.
- Let
![$ f_1,f_2,\dots, f_l \in k[X_0,\dots, X_n]$](img17.png) be homogenious polynomials. Then we set
be homogenious polynomials. Then we set
and call it (the set of 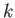 -valued point of) the projective variety
defined by
-valued point of) the projective variety
defined by
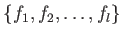 .
.
(Note that the condition
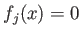
does not depend on the choice of the
representative
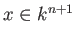
of
![$ [x]\in \P ^n(k)$](img22.png)
.)
LEMMA 3.3
We have the following picture of 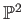 .
.
That means, 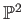 is divided into two pieces
is divided into two pieces
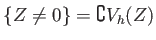 a
nd
a
nd
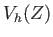 .
.
That means, 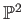 is covered by three “open sets”
is covered by three “open sets”
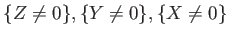 . Each of them is isomorphic to the
plane (that is, the affine space of dimension 2).
. Each of them is isomorphic to the
plane (that is, the affine space of dimension 2).
![]()
![]() , we may
obtain its inhomogenization as follows:
, we may
obtain its inhomogenization as follows:
![]() of degree
of degree ![]() ,
we may
obtain its homogenization as follows:
,
we may
obtain its homogenization as follows: