Congruent zeta functions. No.1
Yoshifumi Tsuchimoto
In this lecture we define and observe some properties of
conguent zeta functions.
For a good brief account of finite fields, consult Chapter I of a book
[1] of Serre.
LEMMA 1.1
For any prime number 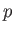 ,
,
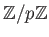 is a field.
(We denote it by
is a field.
(We denote it by
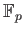 .)
.)
Funny things about this field are:
LEMMA 1.2
Let 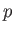 be a prime number.
Let
be a prime number.
Let 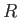 be a commutative ring which contains
be a commutative ring which contains
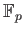 as a subring.
Then we have the following facts.
as a subring.
Then we have the following facts.
holds in 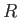 .
.
- For any
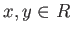 , we have
, we have
We would like to show existence of “finite fields”.
A first thing to do is to know their basic properties.
The next task is to construct such field. An important tool is
the following lemma.
LEMMA 1.4
For any field 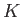 and for any non zero polynomial
and for any non zero polynomial ![$ f\in K[X]$](img17.png) ,
there exists a field
,
there exists a field 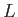 containing
containing 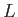 such that
such that
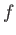 is decomposed into polynomials of degree
is decomposed into polynomials of degree 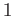 .
.
To prove it we use the following lemma.
Then we have the following lemma.
Finally we have the following lemma.
LEMMA 1.7
Let 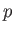 be a prime number. Let
be a prime number. Let 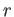 be a positive integer.
Let
be a positive integer.
Let 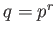 . Then we have the following facts.
. Then we have the following facts.
- There exists a field which has exactly
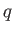 elements.
elements.
- There exists an irreducible polynomial
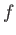 of degree
of degree 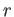 over
over
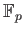 .
.
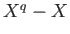 is divisible by
is divisible by 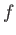 .
.
- For any field
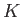 which has exactly
which has exactly 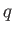 -elements, there exists an element
-elements, there exists an element
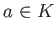 such that
such that 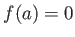 .
.
In conclusion, we obtain:
THEOREM 1.8
For any power 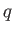 of
of 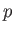 , there exists a field which has exactly
, there exists a field which has exactly 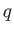 elements.
It is unique up to an isomorphism. (We denote it by
elements.
It is unique up to an isomorphism. (We denote it by
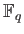 .)
.)
The relation between various
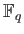 's is described in the following lemma.
's is described in the following lemma.
LEMMA 1.9
There exists a homomorphism from
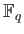 to
to
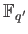 if and only if
if and only if
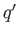 is a power of
is a power of 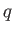 .
.
EXERCISE 1.1
Compute the inverse of
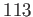
in the field
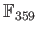
.
![]()
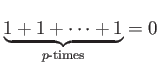
![]() 's is described in the following lemma.
's is described in the following lemma.