Next: About this document ...
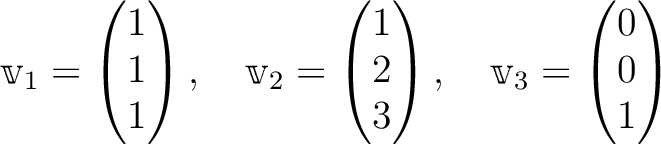
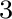
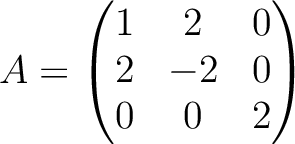 の2つと
直交するものをすべて求めなさい。
そのうちの一つを
の2つと
直交するものをすべて求めなさい。
そのうちの一つを
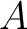 とおく。
とおく。
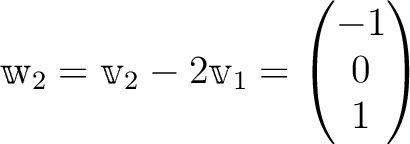 のそれぞれを適当な
定数倍して
のそれぞれを適当な
定数倍して
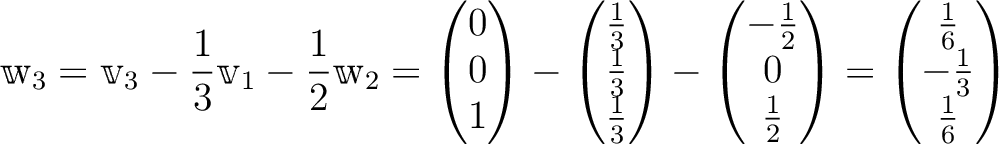 の正規直交基底を作りなさい。
の正規直交基底を作りなさい。
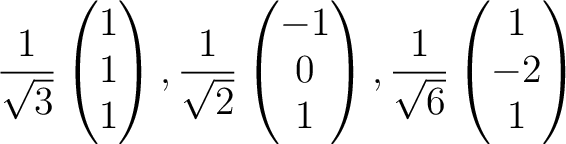
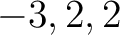 の固有値をすべて求めなさい。
の固有値をすべて求めなさい。
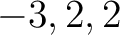 の各固有値に属する固有ベクトル空間をそれぞれ求めなさい。
の各固有値に属する固有ベクトル空間をそれぞれ求めなさい。
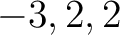 を対角化しなさい。
を対角化しなさい。
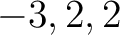 を直交行列を用いて対角化しなさい。
を直交行列を用いて対角化しなさい。
15.1
(1)
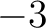
(2)
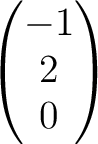
(3)
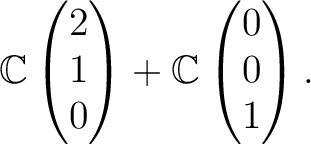
15.2.
(1)
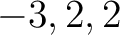 の固有値は
の固有値は 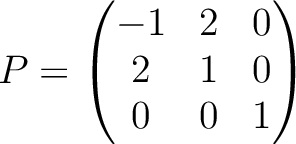 .
.
(2)
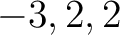 の
の 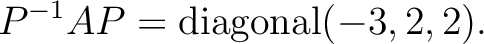 に対する固有ベクトル空間は
に対する固有ベクトル空間は
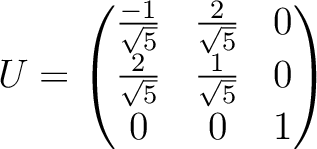 .
.
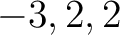 の
の ![]() に対する固有ベクトル空間は
に対する固有ベクトル空間は
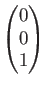
(3)
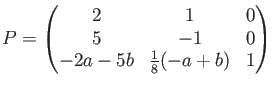
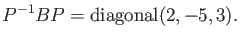
(4)

