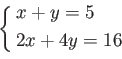
今日のテーマ:連立方程式の解法と行基本操作
連立一次方程式は行列算で表現できる。例えば、
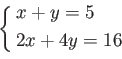
は
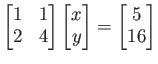
と表現できる。 さらに、
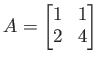 ,
,
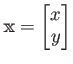 ,
,
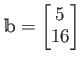 とおけば、
これは更に簡潔に
とおけば、
これは更に簡潔に
更に次のような方程式を考えてみよう。
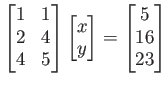
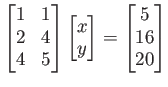
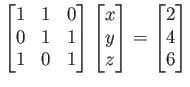
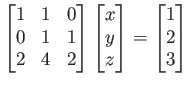
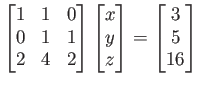
これらの連立方程式は「加減法」によって解けるのであった。 行列でも同じことを行うことができる。行列の行基本操作 とは、
行列は行基本操作を何度も行うことにより、簡単な行列に変形することができる。 このことは、方程式を解くときはもちろん、それ以外の目的でも大変重要である。