Next: Playing with idempotents in Up: , , and the Previous: , , and the
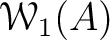 .
Before doing that, we review facts on idempotents.
Recall that an element
.
Before doing that, we review facts on idempotents.
Recall that an element 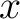 of a ring is said to be idempotent
if
of a ring is said to be idempotent
if 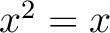 .
.
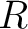 be a commutative ring. Let
be a commutative ring. Let 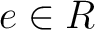 be an idempotent.
Then:
be an idempotent.
Then:
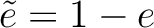 is also an idempotent. (We call it the
complementary idempotent of
is also an idempotent. (We call it the
complementary idempotent of 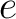 .)
.)
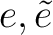 satisfies the following relations:
satisfies the following relations:
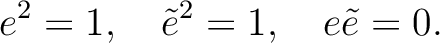
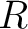 admits an direct product decomposition:
admits an direct product decomposition:
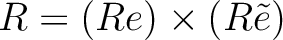
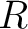 , we define a partial order on the idempotents of if
as follows:
, we define a partial order on the idempotents of if
as follows:

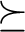 is indeed a partial order.
We note also that, having defined the order on the idempotents,
for any given family
is indeed a partial order.
We note also that, having defined the order on the idempotents,
for any given family
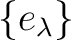 of idempotents we may refer to its “supremum”
of idempotents we may refer to its “supremum”
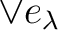 and its“infimum”
and its“infimum”
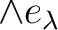 .
(We are not saying that they always exist: they may or may not exist. )
When the ring
.
(We are not saying that they always exist: they may or may not exist. )
When the ring 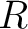 is topologized, then we may
also discuss them by using limits,
is topologized, then we may
also discuss them by using limits,