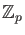 ,
,
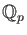 , and the ring of Witt vectors
, and the ring of Witt vectors
No.08:

From here on, we make use of several notions of category theory.
Readers who are unfamiliar with the subject is advised to see
a book such as [#!MacLane2!#] for basic definitions and first properties.
Let 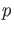 be a prime number.
For any commutative ring
be a prime number.
For any commutative ring 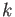 of characteristic
of characteristic 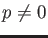 , we want to
construct a ring
, we want to
construct a ring 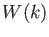 of characteristic 0 in such a way that:
of characteristic 0 in such a way that:
-
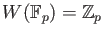 .
.
-
 is a functor. That means,
is a functor. That means,
- For any ring homomorphism
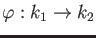 between rings of characterisic
between rings of characterisic 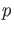 ,
there is given a unique ring homomorphism
,
there is given a unique ring homomorphism
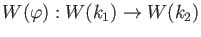 .
.
-
 should furthermore
commutes with compositions of homomorphisms.
should furthermore
commutes with compositions of homomorphisms.
To construct 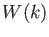 , we construct a new addition and multiplication on a
, we construct a new addition and multiplication on a
 -module
-module
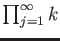 . The ring
. The ring 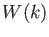 will then be called
the ring of Witt vectors.
The treatment here
essentially follows the treatment which appears in [#!Lang1!#, VI,Ex.46-49],
with a slight modification (which may or may not be good-it may even be wrong)
by the author.
will then be called
the ring of Witt vectors.
The treatment here
essentially follows the treatment which appears in [#!Lang1!#, VI,Ex.46-49],
with a slight modification (which may or may not be good-it may even be wrong)
by the author.
We first introduce a nice idea of Witt.
DEFINITION 08.1
Let
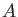
be a ring (of any characteristic).
Let
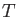
be an indeterminate.
We define the following copy of
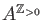
.
(as a set.)
For each element
![$ a(T) \in 1+T A[[T]]$](img17.png) , we will denote by
, we will denote by 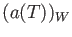 the corresponding element in
the corresponding element in 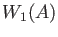 .
.
We will equip
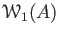 with a ring structure.
To do so we first make use of “log”.
In the following, we use infinite sums and infinite products of elements
of
with a ring structure.
To do so we first make use of “log”.
In the following, we use infinite sums and infinite products of elements
of
![$ \mathcal W_1(A)=1+T A[[T]]$](img21.png) .
They are defined as limits of sums and products with respect to the filtration
topology defined in the usual way.
.
They are defined as limits of sums and products with respect to the filtration
topology defined in the usual way.
LEMMA 08.2
There is an well-defined map
If 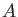 contains an copy of
contains an copy of
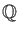 , then the map is a bijection. The inverse is
given by
, then the map is a bijection. The inverse is
given by
PROOF..
To see that
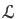
is well defined (that is, “defined over
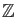
”), we compute
as follows.
The rest should be obvious.
Note: the condition
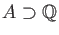 is required to guarantee exictence of
exponential
is required to guarantee exictence of
exponential
and existence of the integration
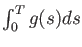 .
.
DEFINITION 08.3
We equip
![$ T A[[T]]$](img32.png)
with the usual addition and the following
(unusual) “coefficient-wise" multiplication:
It is easy to see that
![$ T A[[T]]$](img32.png)
forms a (unital associative)
commutative ring with these binary operations.
DEFINITION 08.4
Let
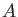
be a ring which contains a copy of
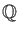
. Then we define ring structure on
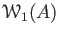
by putting
PROOF..
easy
We may thus extend the definition
 on
on
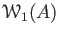 to cases
where the condition
to cases
where the condition
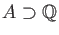 is no longer satisfied.
is no longer satisfied.
We next see that the multiplication of
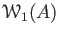 is also
defined over
is also
defined over
 .
To do so, we need the following lemma.
.
To do so, we need the following lemma.
LEMMA 08.6
Let 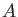 be any commutative ring.
Then every element of
be any commutative ring.
Then every element of
![$ 1+T A[[T]]$](img39.png) is written uniquely as
is written uniquely as
PROOF..
We may use an expansion
to inductively determine
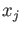
.
More precisely, for each
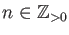
, let us define a polynomial
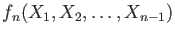
in the following way:
Then for any element
![$ 1+\sum_{j=1}^\infty y_j T^j \in 1+T A[[T]]$](img47.png)
,
we define
Then it is easy to verify that an equation
holds.
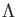
COROLLARY 08.7
![$ {\mathcal W}_1(A)=1+T A[[T]]$](img50.png) is topologically generated by
is topologically generated by
PROOF..
let
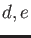
be positive integers. Let
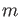
be the least common multiple of
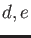
. We have,
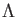
DEFINITION 08.9
Let
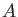
be any commutative ring.
Then we define an addition
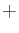
and a multiplication

on
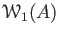
who satisfy the following requirements:
-
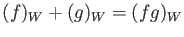 .
.
- For any positive integer
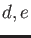 ,
Let
,
Let 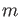 be the least common multiple of
be the least common multiple of 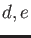 . Then
for any
. Then
for any 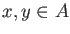 , we have
, we have
- the summation and the multiplication operations are continuous.
(Note that Lemma 8.6 guarantees the
existence and the uniqueness of such multiplication.)
PROOF..
When
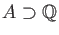
, the statements trivially hold.
This implies in particular that rules such as distributivity
and associativity hold for universal cases
(that means, for formal power series with indeterminate coefficients).
Thus we conclude by specialzation arguments
that the rule also hold for any ring
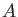
.
DEFINITION 08.11
For any commutative ring
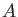
,
elements of
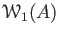
are called
universal Witt vectors over
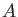
.
The ring
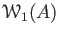
is called
the ring of universal Witt vectors over
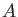
.
PROOF..
We only need to prove the requirement
(2) of Definition
8.9.
With the help of distributive law, the requirement is satisfied if
an equation
|
(#) |
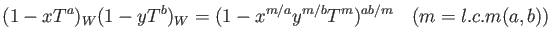 |
holds for each
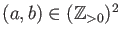
.
To that aim, we first deal with a special case where
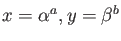 ,
,
![$ A=\mathbb{C}[\alpha,\beta]$](img78.png) ,
,
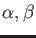 algebraically independent over
algebraically independent over
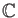 .
In that case we may easily decompose the polynomials
.
In that case we may easily decompose the polynomials 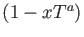 and
and
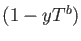 and then we use the distributive law to see that the requirement
actually holds. Indeed, let us put
and then we use the distributive law to see that the requirement
actually holds. Indeed, let us put
and compute as follows.
We second deal with a case where
![$ A=\mathbb{Z}[x,y]$](img90.png) ,
, 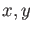 algebraically independent over
algebraically independent over
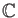 .
In that case we take a look at an inclusion
.
In that case we take a look at an inclusion
and consider
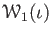
. It is easy to see that
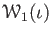
is injection
so that the equation (#) is also true in this case.
The general case now follows from specialization argument.
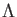

![]() be a prime number.
For any commutative ring
be a prime number.
For any commutative ring ![]() of characteristic
of characteristic ![]() , we want to
construct a ring
, we want to
construct a ring ![]() of characteristic 0 in such a way that:
of characteristic 0 in such a way that:
![]() , we construct a new addition and multiplication on a
, we construct a new addition and multiplication on a
![]() -module
-module
![]() . The ring
. The ring ![]() will then be called
the ring of Witt vectors.
The treatment here
essentially follows the treatment which appears in [#!Lang1!#, VI,Ex.46-49],
with a slight modification (which may or may not be good-it may even be wrong)
by the author.
will then be called
the ring of Witt vectors.
The treatment here
essentially follows the treatment which appears in [#!Lang1!#, VI,Ex.46-49],
with a slight modification (which may or may not be good-it may even be wrong)
by the author.
![$\displaystyle \mathcal W_1(A)=
1+ TA[[T]]
=
\left\{
1+\sum_{j=1}^\infty y_j T^j \ ;\ x_n \in A(\forall n)
\right\}
$](img16.png)
![]() , we will denote by
, we will denote by ![]() the corresponding element in
the corresponding element in ![]() .
. ![]() with a ring structure.
To do so we first make use of “log”.
In the following, we use infinite sums and infinite products of elements
of
with a ring structure.
To do so we first make use of “log”.
In the following, we use infinite sums and infinite products of elements
of
![]() .
They are defined as limits of sums and products with respect to the filtration
topology defined in the usual way.
.
They are defined as limits of sums and products with respect to the filtration
topology defined in the usual way.
![$\displaystyle {\mathcal L}_A=-T\frac{d}{dT}\log(\bullet): 1+T A[[T]] \to T A[[T]].
$](img22.png)
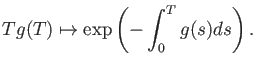
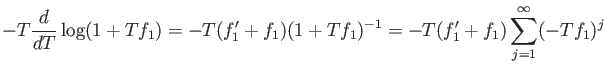
![]() is required to guarantee exictence of
exponential
is required to guarantee exictence of
exponential
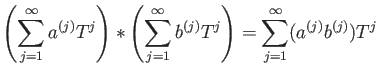
![]() is also
defined over
is also
defined over
![]() .
To do so, we need the following lemma.
.
To do so, we need the following lemma.
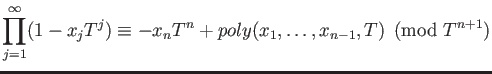
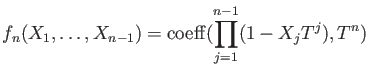
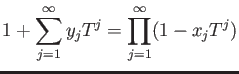
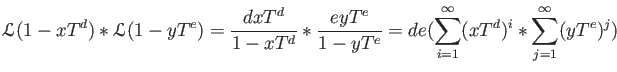
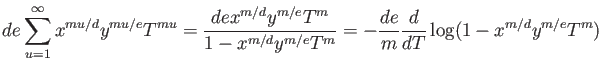
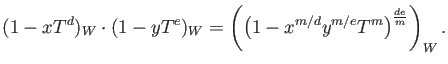
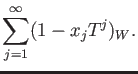
![]()
![]() ,
,
![]() ,
,
![]() algebraically independent over
algebraically independent over
![]() .
In that case we may easily decompose the polynomials
.
In that case we may easily decompose the polynomials ![]() and
and
![]() and then we use the distributive law to see that the requirement
actually holds. Indeed, let us put
and then we use the distributive law to see that the requirement
actually holds. Indeed, let us put
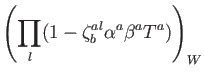
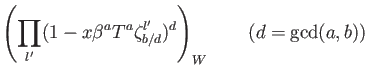
![]() ,
, ![]() algebraically independent over
algebraically independent over
![]() .
In that case we take a look at an inclusion
.
In that case we take a look at an inclusion