線形代数学II No.5要約
今日のテーマ:
直交射影を表す行列
まずは復習から:
- 一次独立なベクトルは「三角変換」(補題3.2のような「三角行列」で書けるような変換)
で直交系に直せた。
- さらに、おのおのの長さで割ることにより、正規直交系を得ることができる。
これがシュミットの直交加法であった。
他方で、
- 内積は、基底
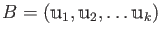 を一つ採るとグラム行列
を一つ採るとグラム行列 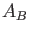 で書くことができる。
グラム行列は
で書くことができる。
グラム行列は
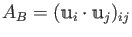 で与えられる
行列であり、
で与えられる
行列であり、
- 内積の関係式は前項の行列算を積み上げる(行列の連結をする)ことで行列の関係式として書くこともできる。
- 正規直交基底に関するグラム行列は単位行列である。(標準的な内積に一致)
以下では、標準的な内積を用いる。
正方行列 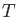 に対して、
に対して、 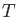 の列ベクトルが正規直交系をなすとき、
の列ベクトルが正規直交系をなすとき、
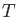 を直交行列と呼ぶ。
を直交行列と呼ぶ。
補題 5.2
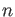 次正方行列
次正方行列 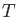 に対して、次は同値である。
に対して、次は同値である。
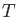 は直交行列
は直交行列
-
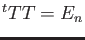
-
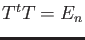
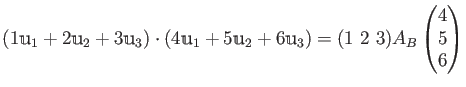
![]() に対して、
に対して、 ![]() の列ベクトルが正規直交系をなすとき、
の列ベクトルが正規直交系をなすとき、
![]() を直交行列と呼ぶ。
を直交行列と呼ぶ。