Next: About this document ...
今日のテーマ:三角関数、指数関数
単位円周上の点 ![]() に対して、
に対して、![]() と、
と、![]() 軸上の正の部分とのなす角を
軸上の正の部分とのなす角を
![]() と書くことにする。(単位は弧度を用いる。)
と書くことにする。(単位は弧度を用いる。) ![]() は
は ![]() の関数と見ることができるので、
の関数と見ることができるので、
図形的性質(原点のまわりに ![]() ラジアン回転して
ラジアン回転して
![]() ラジアン回転したものは
結局
ラジアン回転したものは
結局
![]() ラジアン回転したものである)
により、三角関数の加法定理が従う。
ラジアン回転したものである)
により、三角関数の加法定理が従う。
複素数平面を用いると:
![]() に対して、
に対して、
![]() は
は ![]() を繰り返し掛けることで
定義される。
を繰り返し掛けることで
定義される。
![]() .
整数
.
整数 ![]() と正の整数
と正の整数 ![]() に対して、
に対して、
![]() の 0 での微分係数は
の 0 での微分係数は
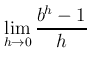
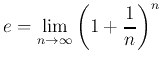
実数 ![]() に対して、次のことが成り立つ:
に対して、次のことが成り立つ:
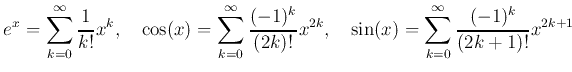
このことさえ知っていれば、最初から
![]() をこの式で定義することも
可能である。さらに、 これを用いると、
をこの式で定義することも
可能である。さらに、 これを用いると、![]() が複素数の範囲であっても
が複素数の範囲であっても
![]() が定義され、
が定義され、