代数学III要約 No.3
今日のテーマ:

定義 3.1
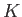
の 拡大体
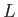
は
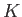
上のベクトル空間の構造を持つ。
そこで、
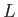
の
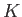
-ベクトル空間としての次元のことを
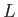
の
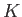
上の
拡大次数 といい、
![$ [L:K]$](img6.png)
で書き表す。
![$ [L:K]<\infty$](img7.png)
のとき、
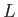
は
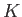
の
有限次拡大であると言う。
定理 3.4
体
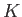
と、その拡大体
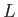
が与えられているとする。
このとき、
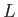
の 元で、
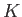
上代数的な元同士の和、差、積、商はまた
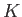
上代数的である。つまり、
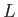
の元で
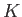
上代数的なものの全体
は体をなす。
定義 3.5
体
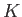
とその拡大体
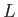
が与えられているとする。このとき
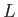
の元
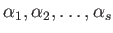
を
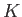
に付け加えてできた体
(言い換えると
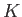
と
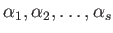
を含むような
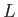
の
部分体のなかで、最小のもの)を
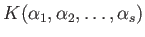
と書く。
(環
![$ K[\alpha_1,\alpha_2,\dots, \alpha_s]$](img17.png)
との違いに注意。)
命題 3.6
体
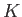
とその拡大体
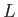
が与えられているとする。このとき
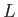
の
代数的な元
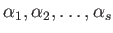
について、次のことが成り立つ。
-
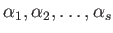 を
を 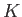 に付け加えてできた体
に付け加えてできた体
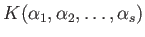 の元はどれも
の元はどれも 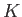 上代数的である。
上代数的である。
問題 3.1
![% latex2html id marker 1033
$ \alpha=\sqrt{2}+7\sqrt[3]{5}$](img19.png)
は
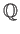
上代数的であることを示しなさい。
![]()
![]() や実数体
や実数体
![]() 以外の体
以外の体 ![]() でも、線形代数で習ったはずの
いろいろな事柄(線形空間、基底とその取り換え、次元。線形写像とその行列表現など)
がそのまま使えることに注意しておく。心配な人はここで少し復習しておくと
良いかもしれない。
でも、線形代数で習ったはずの
いろいろな事柄(線形空間、基底とその取り換え、次元。線形写像とその行列表現など)
がそのまま使えることに注意しておく。心配な人はここで少し復習しておくと
良いかもしれない。