![]() 群の集合への作用と表現
群の集合への作用と表現
のことである。
により作用する。(
により決められる。 更に、正の整数
で定まる。
一般に、任意の有限群 ![]() と任意の素数
と任意の素数![]() に対して、
に対して、
![]() の
の ![]() -シロー群が存在する。(シローの定理)
ここでは、Milne のテキスト
-シロー群が存在する。(シローの定理)
ここでは、Milne のテキスト
http://www.jmilne.org/math/CourseNotes/gt.html を参考にした
証明を述べる。
なお、シローの定理はさらにいくつかの結果を合わせたものを指すのが
普通であるが、それについては、群論の進んだ成書か、上記Milne のテキストを
参照のこと。
このとき、
一般の群 ![]() に対してシローの定理を証明するには、
確実にシロー部分群をもつような群
に対してシローの定理を証明するには、
確実にシロー部分群をもつような群 ![]() に
に ![]() を埋め込めば良い。
そのような群の例としては 有限体
を埋め込めば良い。
そのような群の例としては 有限体
![]() 上の一般線形群などもあるが、
それには少しだけ体論の知識を必要とする。
ここでは
上の一般線形群などもあるが、
それには少しだけ体論の知識を必要とする。
ここでは ![]() を
を
![]() に埋め込むことを考えよう。
に埋め込むことを考えよう。
![]() を大きく取れば埋め込みを作ることは易しい。
を大きく取れば埋め込みを作ることは易しい。
![]() の
の
![]() -シロー群は、つぎのように存在する。
-シロー群は、つぎのように存在する。
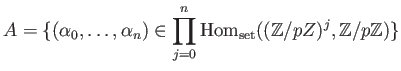
とおき、
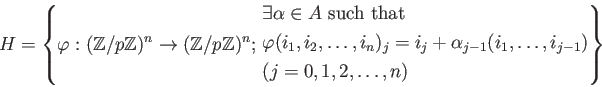
と定義する。このとき: