


Next: About this document ...
1=9
代数学 IA No.9要約
 《正規部分群・剰余群》
《正規部分群・剰余群》
定理 9.1
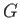
を群、
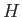
をその部分群とする。
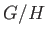
に次のような乗法を定めて群にしてやりたい
。
(
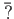
は
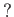
の
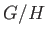
でのクラス。)
これが、
代表元の取りかたによらずにうまくいって、
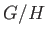
が実際に群にな
るためには、
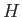
が正規部分群である事が必要十分である。
実際には、「必要十分」のうち、「十分」のほうがよく用いられる。すなわち、
定理 9.2
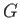
を群、
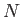
をその正規部分群とする。
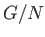
は上の定理の乗法により
群の構造をもつ。
定義 9.3
上の定理で得られる群
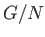
を、
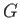
の
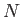
による剰余群(もしくは商群)
とよぶ。
2017-06-12
![]() 《正規部分群・剰余群》
《正規部分群・剰余群》