![]() 《二面体群・正規部分群》
《二面体群・正規部分群》
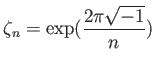 とおく。
複素平面からそれ自身への全単射のうち、
とおく。
複素平面からそれ自身への全単射のうち、
![]() を書き表すにはいくつか方法がある。
を書き表すにはいくつか方法がある。
◎ 生成元と関係式による表示。
![]() の群演算を書き下すには、
の群演算を書き下すには、
![]() があれば良いということが分かる。そのいみで、
があれば良いということが分かる。そのいみで、
と書く。
◎ 置換としての表現
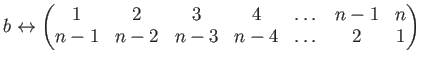
という対応により
◎
実行列としての表示。
![]() はともに
はともに
![]() から
から
![]() への実線形写像であることに着目する。
への実線形写像であることに着目する。
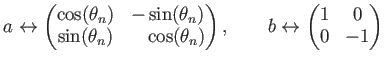
(但し
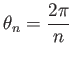 )
)
![]() は非可換な群である。一般に、非可換の群をその部分群で
割る(クラス分けする)際には左、右の別が必要である。
は非可換な群である。一般に、非可換の群をその部分群で
割る(クラス分けする)際には左、右の別が必要である。
のときにいう。これは同値関係を定義する。その同値類の集合を
同様に、右同値、![]() が定義される。
が定義される。
![]() は集合の差の記号
は集合の差の記号
![]() とよく似ているが、
後者は空集合であるからまず使わない。すなわちちょっと考えれば区別がつく。
とよく似ているが、
後者は空集合であるからまず使わない。すなわちちょっと考えれば区別がつく。
右クラス分けは
であり、2つのクラス分けは(実は)一致する。
右クラス分けは
であるが、2つのクラス分けは一致しない。
群 ![]() の剰余類によるクラス分けは、もっと具体的な(例えば、幾何学的な)
意味をもつくことが多い。例えば
の剰余類によるクラス分けは、もっと具体的な(例えば、幾何学的な)
意味をもつくことが多い。例えば
![]() の 例で、
の 例で、