


Next: About this document ...
Up: Algebraic geometry and Ring
Previous: Algebraic geometry and Ring
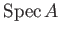
DEFINITION 02.1
An ideal
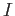
of a ring
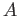
is said to be
- a prime ideal if
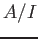 is an integral domain.
is an integral domain.
- a maximal ideal if
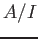 is a field.
is a field.
DEFINITION 02.2
Let
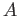
be a ring. Then we define its
affine spectrum as
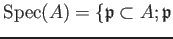
is a prime ideal of $A$
DEFINITION 02.3
Let
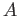
be a ring. For any

we define ``evaluation map''

as follows:
Note that
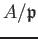 is a subring of a field
is a subring of a field
 , the field of fractions of the integral domain
, the field of fractions of the integral domain
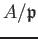 .
We interpret each element
.
We interpret each element 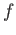 of
of 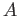 as a something of a ``fuction'',
whose value at a point
as a something of a ``fuction'',
whose value at a point
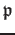 is given by
is given by
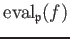 .
.
We introduce a topology on
 . We basically mimic the following
Lemma:
. We basically mimic the following
Lemma:
LEMMA 02.4
Let 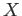 be a topological space.
then for any continuous function
be a topological space.
then for any continuous function
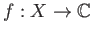 , its zero points
, its zero points
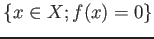 is a closed subset of
is a closed subset of 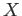 .
Furthermore, for any family
.
Furthermore, for any family
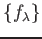 of continous
of continous
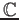 -valued
functions, its common zeros
-valued
functions, its common zeros
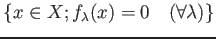 is a closed subset of
is a closed subset of 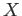 .
.
DEFINITION 02.5
Let
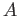
be a ring.
Let
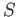
be a subset of
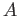
, then we define the common zero of
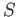
as
For any subset
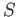
of
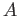
,
let us denote by

the
ideal of
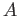
generated by
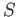
. Then we may soon see that we have
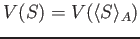
. So when thinking of

we may
in most cases assume that
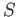
is an ideal of
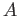
.
PROPOSITION 02.7
Let 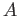 be a ring.
be a ring.
 is an ideal of
is an ideal of 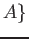 satisfies the axiom of closed sets
of
satisfies the axiom of closed sets
of
 . We call this the Zariski topology of
. We call this the Zariski topology of
 .
.
PROBLEM 02.8
Prove Lemma
2.6.



Next: About this document ...
Up: Algebraic geometry and Ring
Previous: Algebraic geometry and Ring
2017-07-21
![]() is a subring of a field
is a subring of a field
![]() , the field of fractions of the integral domain
, the field of fractions of the integral domain
![]() .
We interpret each element
.
We interpret each element ![]() of
of ![]() as a something of a ``fuction'',
whose value at a point
as a something of a ``fuction'',
whose value at a point
![]() is given by
is given by
![]() .
.
![]() . We basically mimic the following
Lemma:
. We basically mimic the following
Lemma: