が成り立つ。(★)を
今日のテーマ: 行列の対角化。
が成り立つ。(★)を
*上の命題の極限を考えることにより、行列の
![]() も
同様に計算することができる。これは微分方程式の解法などでとくに有用である。
も
同様に計算することができる。これは微分方程式の解法などでとくに有用である。
*話を複素数にまで拡張しておくと、つぎのように単純化される。
*
行列
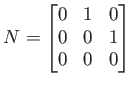 の固有値は
の固有値は ![]() で、固有ベクトルは
で、固有ベクトルは
![]() の
一つだけである。よって
の
一つだけである。よって ![]() は対角化できない。
は対角化できない。
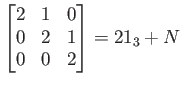 の固有値は
の固有値は ![]() で、対角化できない。
一般の、対角化不可能な行列については、座標変換で「ジョルダンの標準形」までは
持っていくことができる。詳しくは線形代数の進んだ成書を参考のこと。
で、対角化できない。
一般の、対角化不可能な行列については、座標変換で「ジョルダンの標準形」までは
持っていくことができる。詳しくは線形代数の進んだ成書を参考のこと。