


Next: About this document ...
微分積分学基礎 No.3要約
今日のテーマ:(実数区間上の)連続関数
定義 3.1
実数
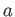
を含む区間上で定義された関数
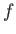
にたいして、
実数
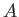
が、
を満たすとき、
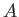
は
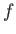
の
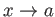
での極限であるといい、
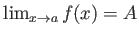
と表記する。
定理 3.2
極限は存在するとすれば一つである。
極限は和、差、積、(分母が0
でない)商をたもつ。
定義 3.3
実数
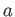
を含む区間
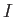
上で定義された関数
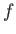
が、
を満たすとき、
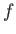
は
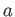
で連続であるという。
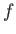
が
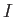
の全ての点で連続であるとき、
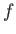
は
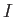
で連続であるという。
命題 3.4
区間
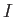
を固定すると、
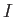
上の 連続関数
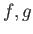
の和、差、積は連続である。I
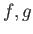
が連続で、
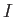
上の各点
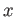
で
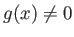
なら、
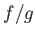
も
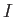
上で連続である。
命題 3.6
区間
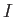
上で関数
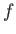
が定義され、
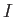
の各点
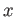
について
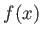
が区間
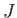
に属するとする。
このとき、
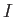
上の関数(
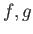
の合成関数)
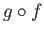
が
で定義される。さらに、
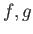
が連続なら
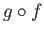
も連続である。
定理 3.7
塀区間
![$ I=[a,b]$](img24.png)
上の連続関数
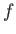
が狭義単調増加であるとする。
すなわち、
と仮定する。このとき、
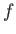
の逆関数
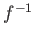
が定義されて、
連続である。
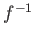
は
![$ J=[f(a),f(b)]$](img27.png)
上定義される関数であって、
任意の
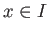
に対し、
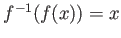
を満たし、
また
任意の
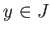
に対し、
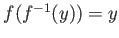
を満たす。



Next: About this document ...
2017-05-01