


Next: About this document ...
代数学 IB No.15要約

命題 15.1
整域 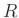 について、次の条件を考える。
について、次の条件を考える。
- (条件1).
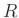 はネーター環である。
はネーター環である。
- (条件2).
- 任意の
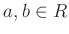 に対して、ある
に対して、ある 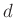 という
という 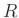 の
元が存在して、
の
元が存在して、 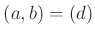 を満たす。
を満たす。
- (条件3).
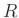 の既約元はすべて素元である。
の既約元はすべて素元である。
このとき、
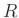 がED であれば、(条件1) と(条件2) が成り立つ。
がED であれば、(条件1) と(条件2) が成り立つ。
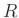 がPID であることは、((条件1) and (条件2)) と同値である。
がPID であることは、((条件1) and (条件2)) と同値である。
- (条件 2) から (条件3)が従う。
- (条件1)and (条件3)から
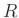 が UFD であることが従う。
が UFD であることが従う。
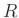 の任意のイデアルが有限個の元で生成される
場合に言うのであった。
の任意のイデアルが有限個の元で生成される
場合に言うのであった。
補題 15.1
ネータ環のイデアルの増大列も、必ずどこかで止まる。
定義 15.1
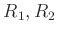
は環であるとする。このとき、
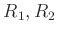
の環としての
直積
とは、デカルト積集合
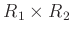
の上に、
次のような演算を定義したものである。
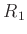
と
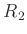
の環としての直積を、普通
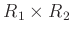
と書く。
補題 15.2
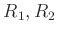 は環であるとする。このとき、
は環であるとする。このとき、
-
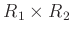 は環になる。
は環になる。
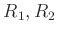 の単位元 がそれぞれ
の単位元 がそれぞれ
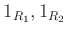 とすると、
とすると、
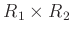 の単位元は
の単位元は
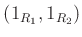 である。
である。
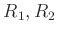 がともに可換ならば、
がともに可換ならば、
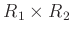 も可換である。
も可換である。
命題 15.2
環 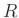 の元
の元 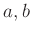 が
が 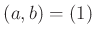 を満たすとき、
を満たすとき、
なる写像は環の同型を与える。
2017-02-02
![]()
![]() の任意のイデアルが有限個の元で生成される
場合に言うのであった。
の任意のイデアルが有限個の元で生成される
場合に言うのであった。