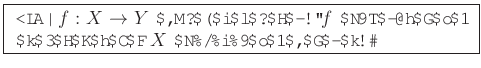1=6 1 by -1    

代数学 IB No.6要約

《準同型と準同型定理》

前回まで、環と、そのイデアルによる剰余環について述べた。 実は、既存の環とそのイデアルを色々と選ぶことにより、 (実用上、全部と言ってもいいぐらい)多くの環を作ることができる。

&dotfill#dotfill;

こんどは、それらの環のあいだの関係が気になるところだ。それを述べるために 必要になるのが、環の準同型の考え方である。

定義 6.1  

$R,S$ はともに(可換とは限らない)環であるとし、$f:R\to S$ をその間の写像とする。 このとき、$f$ が $R$ から $S$ への(環)準同型写像であるとは、次の条件が成り立つ ときにいう。

1. $f$ は $(R,+)$ から $(S,+)$ への群としての準同型である。すなわち、
   $$f(a+b)=f(a)+f(b)$$
   が、すべての $R$ の元 $a,b$ について成り立つ。
2. $f$ は $R$ の積を $S$ の積にうつす。すなわち、
   $$f(ab)=f(a)f(b)$$
   が、すべての $R$ の元 $a,b$ について成り立つ。
3. $f$ は($R$ の)単位元を($S$ の)単位元にうつす。すなわち、
   $$f(1_R)=1_S$$
   が成り立つ。

定義 6.2   環のあいだの全単射準同型のことを、(環としての)同型とよぶ。 容易にわかるように、 環のあいだの同型 $f:R\to S$ が与えられたとき、 $f$ の逆写像 $f^{-1}$ は $S$ から $R$ への 同型になる。

群(加法群)についての準同型の知識を使うと、次のことは直ちにわかる。

補題 6.1   環準同型 $f:R\to S$ について、

1. $f(0_R)=f(0_S)$ が成り立つ。
2. $f(-a)=-f(a)$ が全ての $a\in R$ に対して成り立つ。

つぎに、準同型定理の説明にはいる。

定義 6.3   環準同型 $f:R\to S$ について、 $f^{-1}(0)(=\{r\in R; f(r)=0\})$ のことを、 $f$ の核(Kernel)と呼び、 $\operatorname{Ker}(f)$ で書き表す。

$f$ の像(Image)とは、通常通り、

$$\operatorname{Image}(f)=\{f(r); r\in R\}$$

のことである。

補題 6.2   任意の環準同型 $f:R\to S$ にたいして、

1. $\operatorname{Ker}(f)$ は $R$ のイデアルである。
2. $\operatorname{Image}(f)$ は $S$ の部分環である。

定理 6.1   環準同型 $f:R\to S$ について、 $R$ の同値関係 $\sim_f$ を

$$x \sim_f y \quad {\Leftrightarrow}\quad f(x)=f(y)$$

で定義し、また $r\in R$ の $R/\operatorname{Ker}(f)$ でのクラスを $\bar{r}$ とすると、 次のことが成り立つ。

1. $x,y\in R$ にたいして、
   $$x \sim_f y \quad {\Leftrightarrow}\quad \bar{x}=\bar{y}$$
   が成り立つ
2. $f$ は
   $$\bar{f}:R/\operatorname{Ker}(f) \ni \bar{r} \mapsto f(r)\in \operatorname{Image}(f) \qquad (r\in R)$$
   なる同型を誘導する。

代数では群、加群、環、Lie 環など、いろいろなモノについて それぞれ「準同型定理」がなりたつが、それはすべて次の 単純な事実に基づく:

(I).

環の準同型 $f:{\mbox{${\mathbb{Z}}$}}/12{\mbox{${\mathbb{Z}}$}}\ni [a]_{12} \mapsto [a]_4\in {\mbox{${\mathbb{Z}}$}}/4{\mbox{${\mathbb{Z}}$}}$ ($[?]_n$ は $?$ の ${\mbox{${\mathbb{Z}}$}}/n{\mbox{${\mathbb{Z}}$}}$ におけるクラス) を考える。(本当は、$f$ がうまく定義されていること、 さらに $f$ が実際に環の準同型であることを 諸君が証明すべきだが、ここではそれは要求しない。) このとき、

1. ${\mbox{${\mathbb{Z}}$}}/12{\mbox{${\mathbb{Z}}$}}$ の元 $x$ $12$ 個のそれぞれについて、$f(x)$ を書きなさい。
2. ${\mbox{${\mathbb{Z}}$}}/4{\mbox{${\mathbb{Z}}$}}$ の元 $y$ $4$ 個のそれぞれについて、 $f^{-1}(y)$ を書きなさい。

(II).

${\mbox{${\mathbb{Z}}$}}/11{\mbox{${\mathbb{Z}}$}}\ni [n]_{11}\mapsto [n]_4\in{\mbox{${\mathbb{Z}}$}}/4{\mbox{${\mathbb{Z}}$}}$ はうまく定義されて、 環準同型になるだろうか。