


Next: About this document ...
1=5
1 by -1
代数学 IB No.5要約
 《剰余環、素イデアル、極大イデアル》
《剰余環、素イデアル、極大イデアル》
前回までに、環 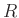 の、そのイデアル
の、そのイデアル 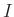 による剰余環について解説した。
による剰余環について解説した。
なる判定法により 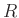 にクラス分けが入ること、
にクラス分けが入ること、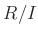 に加法、乗法が
代表元のとり方によらずに定まることがポイントであった。
たとえば
に加法、乗法が
代表元のとり方によらずに定まることがポイントであった。
たとえば
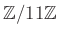 において、
において、
を計算するのに、
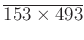 を計算してもよいが、
を計算してもよいが、
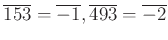 と代表元を取り換えてから
と代表元を取り換えてから
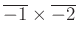 とやっても良いわけである。
とやっても良いわけである。
&dotfill#dotfill;
次のことにも注意しておこう。
一般に、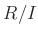 とは環
とは環 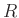 に
に 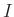 の各元
の各元 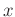 に応じた関係式
に応じた関係式 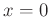 を
新たに導入しててきた環である。例えば:
を
新たに導入しててきた環である。例えば:
-
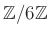 とは、
とは、
 に新たな関係式
に新たな関係式 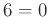 を導入してできた環である。
を導入してできた環である。
-
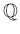
![$ [X]/(X^2-2)$](img17.png) とは、
とは、
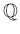
![$ [X]$](img18.png) に新たな関係式
に新たな関係式 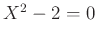 を
導入してできた環である。
を
導入してできた環である。
-
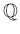
![$ [X,Y]/(X^2-2,XY)$](img20.png) とは、
とは、
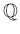
![$ [X]$](img18.png) に新たな関係式
に新たな関係式
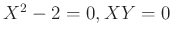 を
導入してできた環である。
を
導入してできた環である。
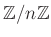 のような剰余環の性質は、いままで知っていた数のものとは若干異なる。
そのことを説明するために、いくつかの言葉を用意しておく。
のような剰余環の性質は、いままで知っていた数のものとは若干異なる。
そのことを説明するために、いくつかの言葉を用意しておく。
定義 5.1
可換環
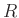
の元
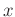
が
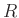
の
零因子であるとは、
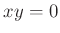
かつ
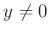
をみたす
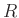
の元
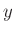
が存在するときに言う。
もちろん、体は必ず整域である。
これらの名前の由来はもっとあとのほうで述べる。
さしあたっては、次の例が重要である。
定義 5.4
素数
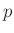
が与えられたとき、
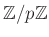
は(上の例に述べたように)元の数が
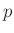
の体である。
この体を
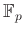
と書く。



Next: About this document ...
2016-10-31
![]() 《剰余環、素イデアル、極大イデアル》
《剰余環、素イデアル、極大イデアル》
![]() の、そのイデアル
の、そのイデアル ![]() による剰余環について解説した。
による剰余環について解説した。
![]() とは環
とは環 ![]() に
に ![]() の各元
の各元 ![]() に応じた関係式
に応じた関係式 ![]() を
新たに導入しててきた環である。例えば:
を
新たに導入しててきた環である。例えば:
![]() のような剰余環の性質は、いままで知っていた数のものとは若干異なる。
そのことを説明するために、いくつかの言葉を用意しておく。
のような剰余環の性質は、いままで知っていた数のものとは若干異なる。
そのことを説明するために、いくつかの言葉を用意しておく。