


Next: About this document ...
1=3
1 by -1
代数学 IB No.3要約
今日のテーマ:
「生成される部分環」を扱った時と同じ議論で、次のことが成り立つことがわかる。
補題 3.1
環 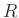 の部分集合
の部分集合 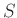 が与えられているとする。このとき、
が与えられているとする。このとき、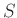 を
含む
を
含む 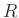 のイデアルのうち、最小のものが存在する。
(これを
のイデアルのうち、最小のものが存在する。
(これを 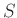 で生成される
で生成される 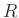 のイデアルといい、
のイデアルといい、
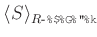 とか、
とか、 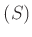 と
書く。)
と
書く。)
上の2つの例を比較すると分かるように、どの環で考えるかが大変重要である。
問題 3.1
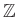
のイデアル
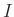
が
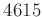
と
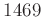
を元として含むとき、
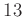
も
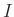
の元であることを示しなさい。
2016-10-14
![]()