第15回目の主題 : 復習と補足。
◎ 同値関係
◯「関係」
◯ クラス分け(分類)をするのに用いられる関係:同値関係
* クラス分けがうまくできるためには守らなければならないルールがある。
それが、推移律、反射律、対称律。
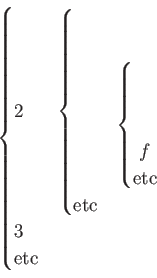
◯ 問題を2つに分ける
◯ 同値関係による等化写像。
集合 ![]() に同値関係
に同値関係 ![]() が定まると、 「等化写像」(「自然な射影」)
が定まると、 「等化写像」(「自然な射影」)
が、各
◎ 部分集合全体の集合。
![]() の部分集合
の部分集合 ![]() は、
は、![]() 上の
上の ![]() のみに値をとる関数
のみに値をとる関数
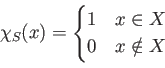
と一対一に対応する。
ところで:
この定義に従うと、![]() の部分集合の全体は
の部分集合の全体は ![]() の元と一対一に対応する
ということになる。そこで:
の元と一対一に対応する
ということになる。そこで:
とくに、 例えば
![]() の部分集合の全部を書きたいとき、
の部分集合の全部を書きたいとき、
![]() と
添え字をつけていたのでは、添字が足りなくなる。そこで
添字集合が必要にな。
と
添え字をつけていたのでは、添字が足りなくなる。そこで
添字集合が必要にな。