

Next: About this document ...
Up: No.07
Previous: No.07
The definition of Artin Mazur zeta function is valid without
assuming the number of the base space 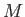 to be a finite set.
to be a finite set.
DEFINITION 07.7
Let
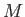
be a set. Let
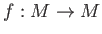
be a map such that
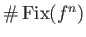
is finite for any
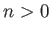
.
We define the Artin-Mazur zeta function of a dynamical system
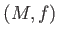
as
Let 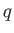 be a power of a prime
be a power of a prime 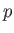 .
We may consider an automorphism
.
We may consider an automorphism
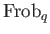 of
of
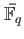 over
over
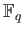 by
by
PROPOSITION 07.8
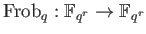 is an automorphism of order
is an automorphism of order 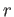 .
It is a generator of the Galois group
.
It is a generator of the Galois group
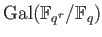 .
.
For any projective variety 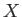 defined over
defined over
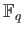 ,
we may define a Frobenius action
,
we may define a Frobenius action
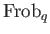 on
on
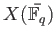 :
:
For any
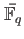 -valued point
-valued point
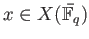 , We have
, We have
PROPOSITION 07.9
The Artin Mazur zeta function of the dynamical system
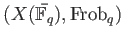 conincides with the congruent zeta function
conincides with the congruent zeta function
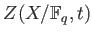 .
.


Next: About this document ...
Up: No.07
Previous: No.07
Yoshifumi Tsuchimoto
2016-06-18
![]() to be a finite set.
to be a finite set.
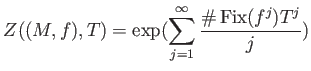
![]() be a power of a prime
be a power of a prime ![]() .
We may consider an automorphism
.
We may consider an automorphism
![]() of
of
![]() over
over
![]() by
by
![]() defined over
defined over
![]() ,
we may define a Frobenius action
,
we may define a Frobenius action
![]() on
on
![]() :
:
![]() -valued point
-valued point
![]() , We have
, We have