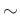 は同値関係であることを示しなさい。
は同値関係であることを示しなさい。
- 以下この問題では、
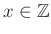 の
の 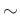 に関するクラスを
に関するクラスを ![$ [x]$](img5.png) と書く。
と書く。
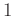 のクラス
のクラス ![$ [1]$](img7.png) に属する
に属する
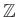 の元をすべて答えなさい。
の元をすべて答えなさい。
-
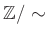 から
から
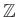 への写像
への写像 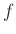 を、
を、
![$ f([x])=$](img10.png) ($x$ を $3$ で割った余り)
で定義できるだろうか。
($x$ を $3$ で割った余り)
で定義できるだろうか。
-
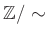 から
から
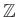 への写像
への写像 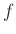 を、
を、
![$ f([x])=$](img10.png) ($x$ を $4$ で割った余り)
で定義できるだろうか。
($x$ を $4$ で割った余り)
で定義できるだろうか。
第13回目の主題 : 「代表元のとり方によらない」
|
一般に、集合
をみたすとき、
により定義できる。 |
つぎのことは集合の準同型定理とも呼ばれ、線形代数学、代数学などの各分野で 基本的な役割を果たす。
により定義される。
によりうまく定義される。 ここに、