第4回目の主題 :
![]()
まずは論理の復習
論理復習ここまで
集合の関係を論理で述べることもよくある。
は正しいだろうか?
集合と論理とは裏腹の関係にあるのであった。論理の ![]() や
や ![]() に対応する集合論的な概念も存在する。
に対応する集合論的な概念も存在する。
同様に、集合 ![]() の一つ一つの元
の一つ一つの元 ![]() に対して集合
に対して集合 ![]() が与えられたとき、集合の族
が与えられたとき、集合の族
![]() が与え
られたという。
が与え
られたという。![]() のことをこの族の添字集合と呼ぶ。
のことをこの族の添字集合と呼ぶ。
もちろん集合列は集合族の特別な場合である。
![]() のことを
のことを
![]() のように書いているのである。
のように書いているのである。
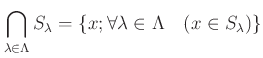
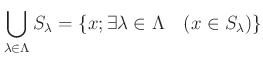
により定義する。
集合列については、その共通部分
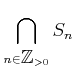
のことを
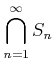
のごとく書くことも多い。和集合も同様。
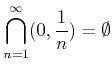
であることを示しなさい。 右辺の記号は空集合といって、元をひとつも持たない集合のことをさす 記号である。
![$\displaystyle \bigcap_{\epsilon>0} (-\infty, 1+\epsilon) =(-\infty, 1]
$](img25.png)
であることを示しなさい。 (左辺は堅苦しく書けば
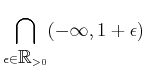 となるところであるが、上のように省略することが往々にしてある。)
となるところであるが、上のように省略することが往々にしてある。)