


Next: About this document ...
代数学 IA No.14要約
 群の直積 (+準同型定理の応用)
群の直積 (+準同型定理の応用)
定義 14.1 (群の直積)
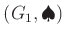
と、
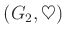
とが共に群であるとする。このとき、デカルト積集合
は、次のような演算
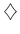
により群になる。
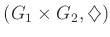
を
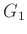
と
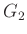
の(群としての)直積と呼ぶ。
定理 14.3 (有限巡回群の直積分解)
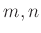
を互いに素な正の整数とする。このとき、同型
が存在する。
系 14.4
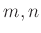
を互いに素な整数とすると、
となる整数
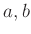
が存在する。
この系自身もよく利用される。応用例として一つだけ挙げておく。
系 14.5 (系の系)
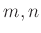
を互いに素な正の整数とする。このとき、
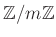
の、
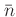
で生成される
部分群は、
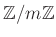
自身である。
◎群と群準同型の作り方について。
-
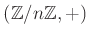 から 群
から 群 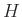 への群準同型を作るには、
への群準同型を作るには、
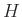 の元
の元 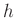 (``
(``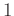 の行き先'')で、
の行き先'')で、
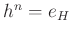 をみたすものを作ればよい。
をみたすものを作ればよい。
- 上のことは、次のように一般化できる。
正の整数
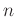 に対して、
に対して、
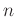 個の元
個の元
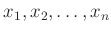 で生成される自由群
で生成される自由群
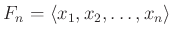 が存在する。
が存在する。
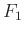 は
は
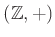 と同型である。(
と同型である。(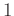 が
が 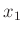 の役割をする。)
の役割をする。)
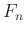 から他の群への群準同型を与えることは、
から他の群への群準同型を与えることは、
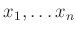 の行き先
を与えることと同じである。
の行き先
を与えることと同じである。
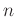 個の元で生成された群
個の元で生成された群
は、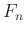 を、
(関係式)
を、
(関係式)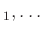 (関係式)
(関係式)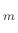 (の "g" を "x" で
置き換えたもの) で生成された正規部分群
(の "g" を "x" で
置き換えたもの) で生成された正規部分群 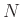 で割った剰余群と同型である。
で割った剰余群と同型である。
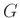 から
から 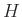 への群準同型は、
への群準同型は、
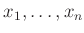 の行き先
の行き先
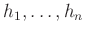 で、
(関係式)
で、
(関係式)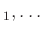 (関係式)
(関係式)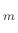 (の "g" を "h" で
置き換えたもの)が成り立つものを与えれば良い。
(の "g" を "h" で
置き換えたもの)が成り立つものを与えれば良い。
問題
- (I).
-
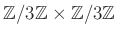 は 巡回群ではないことを証明しなさい。
は 巡回群ではないことを証明しなさい。
2015-07-16
![]() 群の直積 (+準同型定理の応用)
群の直積 (+準同型定理の応用)