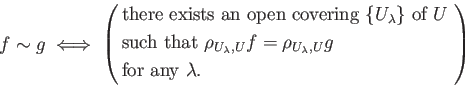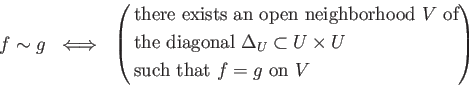Next: sheafification of a sheaf
Up: zeta functions
Previous: homomorphisms of (pre)sheaves
To proceed our theory further, we need to study a bit more about presheaves.
Unfortunately, a sheaf of modules 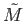 on an affine schemes are ``too good''. Namely,
in terms of cohomology (which we study later,) we have always
on an affine schemes are ``too good''. Namely,
in terms of cohomology (which we study later,) we have always
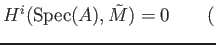
if
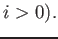
So to study some important problems on sheaf theory (which we
will sure to encounter when we deal with non-affine schemes,)
we need to study some examples from other mathematical areas.
A first example is a presheaf which satisfies the ``locality'' of sheaf axiom,
but which fails to obey ``gluing lemma''.
EXAMPLE 10.18
Let

be the (usual) real line with the usual Lebesgue measure.
Then we have a presheaf of
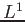
-functions given by
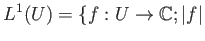
is integrable
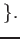
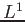
is a presheaf which satisfies the ``locality'' of sheaf axiom,
but which fails to obey ``gluing lemma''.
Indeed, Let
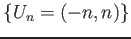
be an open covering of
and define
a section
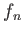
on
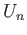
by
Then we see immediately that
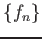
is a family of sections which satisfies
the assumption of ``gluing lemma''. The function which should
appear as the ``glued function'' is the constant function
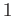
, which
fails to be integrable on the whole of
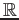
.
We may ``sheafificate'' the presheaf 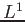 above.
Instead of
above.
Instead of 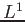 -functions we consider functions which are locally
-functions we consider functions which are locally 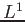 .
Namely, for any open subset
.
Namely, for any open subset
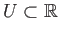 , we consider
, we consider
The presheaf so defined is a sheaf, which we may call ``the sheaf of
locally
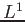
-functions''.
EXAMPLE 10.19
Similarly, we may consider a presheaf
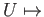
Bdd
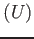
of bounded functions on a topological
space
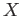
. We may sheafificate this example and the sheaf so created is
the sheaf of locally bounded functions.
EXAMPLE 10.20
It is psychologically a bit difficult to give an example of
a presheaf which does not satisfy the locality axiom of a sheaf.
But there are in fact a lot of them.
For any differentiable (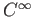 ) manifold
) manifold 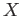 (students
which are not familiar with the manifolds may take
(students
which are not familiar with the manifolds may take 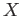 as an open
subset of
as an open
subset of
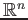 for an example.),
we define a presheaf
for an example.),
we define a presheaf
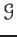 on
on 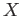 defined as follows
defined as follows
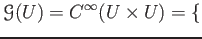
complex valued $C^&infin#infty;$-functions on $U×U$
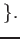
The restriction is defined in an obvious manner.
It is an easy exercise to see that the presheaf does not satisfy the
locality axiom of a sheaf.
To sheafificate this, we first need to introduce an equivalence relation on
 .
.
Then we may easily see that
holds.
Then we define
It is now an easy exercise again to verify that
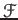
so defined
is a sheaf.
(Readers who are familiar with the theory of jets may notice that
the sheaf is related to the sheaf of jets. In other words, there is a
sheaf homomorphism from this sheaf to the sheaf of jets.)



Next: sheafification of a sheaf
Up: zeta functions
Previous: homomorphisms of (pre)sheaves
2015-06-29
![]() above.
Instead of
above.
Instead of ![]() -functions we consider functions which are locally
-functions we consider functions which are locally ![]() .
Namely, for any open subset
.
Namely, for any open subset
![]() , we consider
, we consider
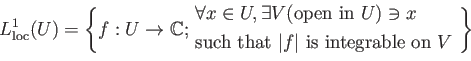
![]() ) manifold
) manifold ![]() (students
which are not familiar with the manifolds may take
(students
which are not familiar with the manifolds may take ![]() as an open
subset of
as an open
subset of
![]() for an example.),
we define a presheaf
for an example.),
we define a presheaf
![]() on
on ![]() defined as follows
defined as follows
![]() .
.