Fourier analysis tells us that the function space on
Let us consider the Laplacian
The 0 -eigenspace of the Laplacian corresponds to the space of constants
We may then consider its
Its trace is equal to the Riemann Zeta function (up to the multiplicative constant
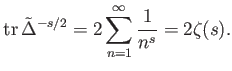
In general, we employ the following principle:
The zeta functions are ``generating functions of number of particles''
The meaning of the term ``particles'' may vary.