


Next: About this document ...
代数学 IB No.10要約
 《素元分解環》
《素元分解環》
「素因数分解の一意性」が成り立つような環を素元分解環と呼ぶ。
ただし、
のような無用の分解を避けるために、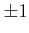 に類するもの(可逆元)を特別扱いする
ことにする。
に類するもの(可逆元)を特別扱いする
ことにする。
定義 10.1
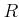
は環であるとする。
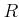
の元のうち、
積に関して可逆なもの(可逆元)の全体を
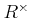
であらわす。
環論においては、元 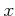 の性質を調べる代わりに、
の性質を調べる代わりに、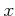 の生成するイデアル
の生成するイデアル 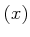 を調べるとうまくいくことがある。以下の議論でも頻繁に使われるので
注意しておくとよい。
歴史的には、一般の環では元だけの扱いに限界があって、イデアルを導入すると
うまくいくということに Dedekind が気付き、そこで展開されたイデアル論に
古典的な幾つかの議論が吸収されたのだ。
を調べるとうまくいくことがある。以下の議論でも頻繁に使われるので
注意しておくとよい。
歴史的には、一般の環では元だけの扱いに限界があって、イデアルを導入すると
うまくいくということに Dedekind が気付き、そこで展開されたイデアル論に
古典的な幾つかの議論が吸収されたのだ。
定義 10.2
可換環
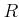
の元
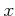
が素元であるとは、
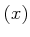
が
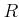
の素イデアルであるときにいう。
例えば、
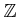 ,
,
![$ {\mathbb{C}}[X]$](img17.png) は素元分解環である。もっと一般に、
次のことが成り立つ。
は素元分解環である。もっと一般に、
次のことが成り立つ。
定理 10.1
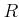 が単項イデアル整域ならば、
が単項イデアル整域ならば、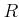 は素元分解環である。
は素元分解環である。
この定理の証明(今週と来週)はいくつかの段階にわかれる。
まず、次の事実の拡張からはじめよう。
事実 10.1
整数 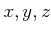 があって、
があって、 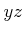 は
は 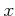 で割り切れ、
かつ
で割り切れ、
かつ 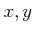 が互いに素であるとする。このとき、
が互いに素であるとする。このとき、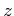 は
は 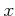 で割り切れる。
で割り切れる。
整数 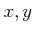 が互いに素なら、
が互いに素なら、
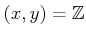 であったことを思い起こすと、
次の補題は上の事実の拡張であることが分かるだろう。
であったことを思い起こすと、
次の補題は上の事実の拡張であることが分かるだろう。
補題 10.2
可換環 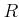 の元
の元 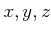 があって、
があって、 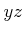 は
は 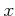 で割り切れ、かつ
で割り切れ、かつ
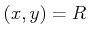 であるとする。このとき、
であるとする。このとき、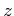 は
は 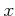 で割り切れる。
で割り切れる。
定義 10.4
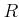
は可換環であるとする。
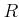
の元
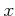
が既約であるとは、
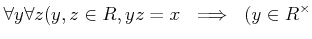
または
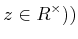
のときに言う。
補題 10.3
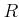 は整域であるとする。このとき、
は整域であるとする。このとき、
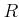 の素元は、必ず既約である。
の素元は、必ず既約である。
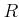 の既約元は、必ずしも素元とは限らない。
の既約元は、必ずしも素元とは限らない。
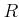 が単項イデアル環で、なおかつ整域ならば、
が単項イデアル環で、なおかつ整域ならば、
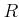 の既約元は必ず素元である。
の既約元は必ず素元である。
上の補題により、単項イデアル整域 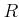 の元
の元 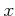 を素因数分解する手順は
次のようになる。
を素因数分解する手順は
次のようになる。
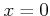 または
または
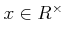 ならば、おしまい。
ならば、おしまい。
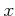 が素元ならば、やはりおしまい。
が素元ならば、やはりおしまい。
- それ以外なら、
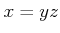 (
(
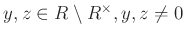 )と
分解できる。
)と
分解できる。
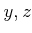 について同様のことをする。
(例えば
について同様のことをする。
(例えば 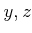 が 素元でなければ、
が 素元でなければ、 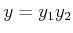 となる。)
となる。)
- 繰り返す。
あとの問題は、一つの元が無限に分解されていかないか、ということである。
次の補題がその問題に答える:
補題 10.4
単項イデアル環 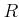 のイデアルの増大列
のイデアルの増大列
は必ずどこかで止まる。すなわちある 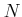 があって、
があって、
がなりたつ。
(参考)
![$ {\mathbb{C}}[X]$](img17.png) の部分環
の部分環
![$ R={\mathbb{C}}[X^2,X^3]$](img34.png) を考えると、
を考えると、
![$\displaystyle R=\{f\in {\mathbb{C}}[X];$](img35.png)
$f$ の $X$ に関する一次の項の係数は $0$
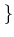
であることが分かる。ここで、
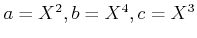 とおくと、
とおくと、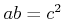 であるが、
であるが、
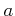 は
は 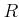 のなかで既約である
のなかで既約である
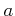 は
は 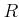 のなかで
のなかで 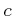 の約数ではない。
の約数ではない。
ということが分かる。このように、単に「環」といってもこのような「特異な」環も
含まれるので、その元の取り扱いには通常の整数を取り扱う以上の注意が必要である。
![% latex2html id marker 1266
$ {\mbox{${\mathbb{Z}}$}}[\sqrt{5}] $](img40.png) のなかの
のなかの
なども、素因数分解の非一意性の例である。
問題 10.1
素元分解環
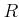
の元
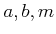
について、
が成り立つことを示しなさい。
ヒント: 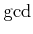 の定義
の定義
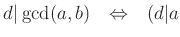
かつ
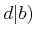
を有効に使うこと。
問題 10.2
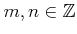
が
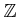
において互いに素(すなわち、
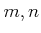
の最大公約数が
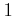
)
ならば、
![% latex2html id marker 1299
$ {\mbox{${\mathbb{Z}}$}}[\sqrt{-1}]$](img50.png)
の元としても互いに素であることを
証明せよ。
問題 10.3
![% latex2html id marker 1306
$ {\mbox{${\mathbb{Z}}$}}[\sqrt{-1}]$](img51.png)
が素元分解環であることをもちいて、
互いに素な
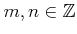
に対して
![% latex2html id marker 1310
$ {\mbox{${\mathbb{Z}}$}}[\sqrt{-1}]$](img52.png)
の元として
が成り立つことを示しなさい。



Next: About this document ...
2014-12-19
![]() 《素元分解環》
《素元分解環》
![]() の性質を調べる代わりに、
の性質を調べる代わりに、![]() の生成するイデアル
の生成するイデアル ![]() を調べるとうまくいくことがある。以下の議論でも頻繁に使われるので
注意しておくとよい。
歴史的には、一般の環では元だけの扱いに限界があって、イデアルを導入すると
うまくいくということに Dedekind が気付き、そこで展開されたイデアル論に
古典的な幾つかの議論が吸収されたのだ。
を調べるとうまくいくことがある。以下の議論でも頻繁に使われるので
注意しておくとよい。
歴史的には、一般の環では元だけの扱いに限界があって、イデアルを導入すると
うまくいくということに Dedekind が気付き、そこで展開されたイデアル論に
古典的な幾つかの議論が吸収されたのだ。
![]() ,
,
![]() は素元分解環である。もっと一般に、
次のことが成り立つ。
は素元分解環である。もっと一般に、
次のことが成り立つ。
![]() の元
の元 ![]() を素因数分解する手順は
次のようになる。
を素因数分解する手順は
次のようになる。
![]() の部分環
の部分環
![]() を考えると、
を考えると、
![]() のなかの
のなかの