微分積分学概論AI要約 No.12

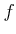
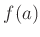
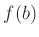
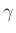
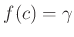
定理 12.1 (中間値の定理)   (再) 関数 $f$ が閉区間 $[a,b]$ で連続(すなわち、$[a,b]$ の各点で連続)とする。 このとき $f(a)$ と $f(b)$ の中間の値 $\gamma$ にたいして、 $f(c)=\gamma$ をみたすような $c\in [a,b]$ が存在する。

定理 12.2 (再)   有界閉区間 $[a,b]$ 上の連続関数は必ず最大値を持つ。

この定理は位相空間論においては「コンパクト集合の像は コンパクトである」という定理(あるいはその系の「コンパクト集合上の 連続関数は最大値を持つ」という定理) に一般化される。

問題 12.1  

1. 閉区間 $[0,1]$ 上で定義された実数値連続関数 $f(x),g(x)$ が、 任意の $x\in [0,1]$ にたいして $f(x)>g(x)$ をみたすとき、 ある正の数 $\epsilon_0$ が存在して、 $f(x)\geq g(x)+\epsilon_0$ がすべての $x\in [0,1]$ に対して 成り立つことを示しなさい。
2. 上で、閉区間 $[0,1]$ のところを開区間 $(0,1)$ に 置き換えた場合にはどのような ことが起こるだろうか。