![]()
がなりたつときにいう。
極限の定義により、上の定義は次のように言い換えられる。
![]()
上の定理は「定理」ではあるが、
連続性の定義における ``![]() '' の「例外的な扱い」を取り除いてむしろ
自然な形をしている。そこでこの講義ではもっぱら連続性を確かめるには
上の定理のほうを用いて判定することにする。実際には、関数
'' の「例外的な扱い」を取り除いてむしろ
自然な形をしている。そこでこの講義ではもっぱら連続性を確かめるには
上の定理のほうを用いて判定することにする。実際には、関数 ![]() が
が
![]() の近くで定義されているという前提条件は強すぎる。そこで
定義域についての条件をハッキリ記述して次のように定義しよう。
の近くで定義されているという前提条件は強すぎる。そこで
定義域についての条件をハッキリ記述して次のように定義しよう。
(☆)
![]()
を満たすときに言う。
![]() を明示することにより、
を明示することにより、![]() の動く範囲に関する制限が明確になる。
とくに
の動く範囲に関する制限が明確になる。
とくに ![]() が
が
![]() のときを考えれば「右連続性」(``§4(I)'')
が自然に解釈できる。
のときを考えれば「右連続性」(``§4(I)'')
が自然に解釈できる。
上の定義で、 ![]() は
は ![]() と
と ![]() の距離、
の距離、
![]() は
は ![]() と
と
![]() の距離であることに注意する。上の連続性の定義は
多変数関数や、距離空間のあいだの写像の連続性の定義に
そのまま一般化することができる。
の距離であることに注意する。上の連続性の定義は
多変数関数や、距離空間のあいだの写像の連続性の定義に
そのまま一般化することができる。
(☆)の否定、すなわち、 「![]() が
が ![]() で連続でない」ことは、
次のように書き表すことができる。
で連続でない」ことは、
次のように書き表すことができる。
(★)
![]() かつ
かつ ![]()
この講義では三角関数については完全な取り扱いができない予定なので、 例題やレポート問題においてはいくつかのことは高校までの知識を援用して、 証明なしに用いることにする。 ただし、それぞれの段階でどのようなことを使ったかは明確にしておきたい。
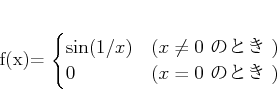
で定義するとき、
関数
![]()
![]()
![]()
![]() を
を
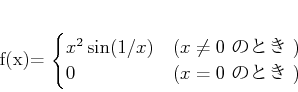
で定義するとき、
補遺: 部分列について
数列の収束について、次のことを補足しておく。
余力のある人は、(2)において、「部分列の収束先がどれでも一緒である」 と仮定しなくても良いところにも注目すると良い。