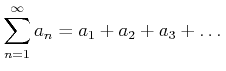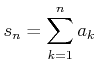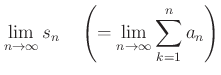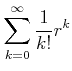Next: About this document ...
微分積分学概論AI要約 No.7
第7回目の主題 :

数列
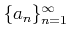 に対して、
形式的な和
に対して、
形式的な和
のことを級数とよぶ。このように形式的に
決めたからと言って、その「値」が何もせずに決まるわけではない。
上の級数について、
で定義される 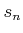 のことをこの級数の部分和と呼ぶ。
部分和からできた数列
のことをこの級数の部分和と呼ぶ。
部分和からできた数列 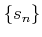 が収束するとき、
が収束するとき、
で定義される数をこの級数の和と呼ぶ。
定義 7.1
各
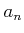
が 0
以上の時の級数
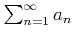
のことを
正項級数とよぶ。
有界な単調列は収束することから、次のことが分かる。
命題 7.2
正項級数は、部分和からなる列が有界ならば必ず収束する。
正項級数に限らない級数については、絶対収束の概念が大事である。
定理 7.3
級数
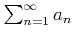
は、
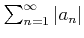
が収束すれば収束する。
定義 7.4
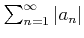
が収束するとき、
級数
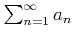
は、
絶対収束すると呼ばれる。
「絶対収束する」というのはひとまとまりでひとつの数学用語である。
あえて言えば「絶対値の和が収束している」という言葉の省略に近い。
「絶対に収束する」という言葉とはまったく異なる。
例 7.6
任意の実数
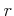
に対して、
は収束する。この和を
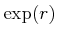
と書く。
2014-05-26
![]()
![]() に対して、
形式的な和
に対して、
形式的な和