論理と集合要約 No.6

第6回目の主題 :

集合を扱う際は 個々の元を取り出し、 諸性質を論理で証明する。

例えば、 $A=6{\mbox{${\mathbb{Z}}$}}$ , $B=2{\mbox{${\mathbb{Z}}$}}$ にたいして、 $A \subset B$ を示すには、

1. $A$ の各元 $x$ について、
2. $x=6 n =2 (3 n)$ であることを示し、
3. $x=2(3n)\in B$ と結論する。

というステップを踏むのだった。

同様に、 $A_2=\{ x\in$$\mbox{${\mathbb{R}}$}$$\vert x>20 \}$ , $B_2=\{x\in$   $\mbox{${\mathbb{R}}$}$$\vert x^4 -7 x -9 >0\}$ に対して、 $A_2 \subset B_2$ を示すには、

1. $A_2$ の各元 $x$ について、

2. $$x^4-7x-9 \geq x^4 - 10 x^3 -10 x^3 \geq x^3 (x-20) > 0$$
   であることを示し、
3. $x\in B_2$ と結論する。

と良い。

問題 6.1   実係数の多項式 $f(x)=a_n x^n+a_{n-1} x^{n-1}+ \dots +a_1 x + a_0$ が、 $a_n>0$ を満たすとする。 $M= \frac{n}{a_n}\max\{a_{n-1} ,a_{n-2},\dots, a_0\}$ とおくと、

$$\{ x \in$$   $$\mbox{${\mathbb{R}}$}$$$$\vert x >M \} \subset \{x \in$$   $$\mbox{${\mathbb{R}}$}$$$$\vert f(x) >0\}$$

が成り立つことを示しなさい。

集合の一般論でも同様。

問題 6.2   集合 $A,B,C,D$ に対して、

$$(A \subset C$$$$\text { and } B \subset D )\implies A\cup B \subset C \cup D$$

を示しなさい。

問題 6.3   集合 $X,Y,Z$ に対して、 $X \subset Y \implies Z \setminus X \subset Z \setminus Y$ を示しなさい。

問題 6.4   集合族 $\{A_i\}, \{B_i\}$ が与えられた時、包含関係

$$(\cup A_i) \setminus (\cup B_i) \subset \cup (A_i \setminus B_i)$$

および

$$(\cap A_i) \setminus (\cap B_i) \supset \cap (A_i \setminus B_i)$$

を示しなさい、

&dotfill#dotfill;

$v=(v_1,v_2,\dots,v_n) \in$   $\mbox{${\mathbb{R}}$}$$^n$ にたいし、そのノルムを

$$\vert\vert v\vert\vert=\sqrt{v_1^2+v_2^2+ \dots + v_n^2}$$

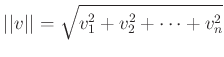
で定義する。このとき、 $v=(v_1,v_2,\dots,v_n) \in$   $\mbox{${\mathbb{R}}$}$$^n$ , $w=(w_1,w_2,\dots, w_n)$ にたいして、

$$\vert\vert v+w\vert\vert \leq \vert\vert v\vert\vert +\vert\vert w\vert\vert$$

がなりたつ。(三角不等式。)

一般に、 $a\in$   $\mbox{${\mathbb{R}}$}$$^n$ と $r>0$ に対して、

$$B_r(a)=\{ x \in$$   $$\mbox{${\mathbb{R}}$}$$$$^n; \vert\vert x-a\vert\vert< r\}$$

$$\bar{B}_r(a)=\{ x \in$$   $$\mbox{${\mathbb{R}}$}$$$$^n; \vert\vert x-a\vert\vert\leq r\}$$

とおく。

$\mbox{${\mathbb{R}}$}$$^n$ の部分集合 $U$ は

$$\forall x \in U \exists r \in$$   $$\mbox{${\mathbb{R}}$}$$$$_{>0} \quad B_r(x) \subset U$$

を満たすとき、(通常位相に関して)開集合であると呼ばれる。 開集合とは、「境界を含まない集合」ということの数学的な表現である。

開集合というものをベースにして、「遠い」「近い」「つながっている」などの 概念を数学的に取り扱えるようにしたものが位相空間論である。 位相空間論は現代数学において大変重要な位置を占めていて、 進んで数学を学びたい人は、例えば微分積分学の学習と並行して学習してみるのも オススメである。

「境界」という言葉自体も数学的に表現できるが、 ここではそこまでは踏み込まないことにする。

問題 6.5   開球 $B_1(0)$ は開集合であることを示しなさい。

問題 6.6   閉球 $\bar{B}_1(0)$ は開集合ではないことを示しなさい。

問題 6.7   $\mbox{${\mathbb{R}}$}$$^2$ の部分集合 $\{(x,0) ; x \in$   $\mbox{${\mathbb{R}}$}$$\}$ は開集合ではないことを示しなさい。

問題 6.8   任意の $a,b \in$   $\mbox{${\mathbb{R}}$}$$^n$ と任意の正の数 $r_1,r_2$ にたいして、 $B_ {r_1}(a)\cap B_{r_2}(b)$ は開集合であることを示しなさい。

問題 6.9   任意の

$$\bigcap_{n=1}^\infty B_{1+1/n} (0)=\bar B_1(0)$$

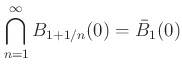
であることを示しなさい。

一般に、開集合の２つの共通部分は開集合だが、 無限個の共通部分は開集合とは限らない。