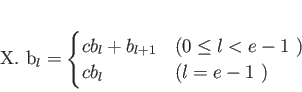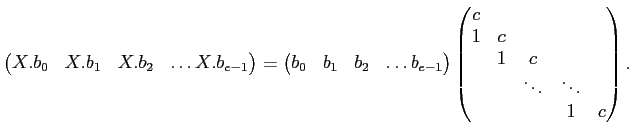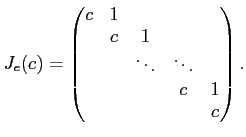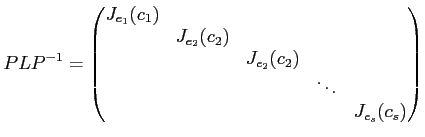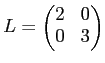Next: About this document ...
代数学II要約 No.11
今回は、行列のジョルダンの標準形について PID 上の加群の理論の立場から
概説しよう。つぎのような基本仮定を出発点とする。
![\begin{itembox}[l]{基本仮定}
$k$\ は体であるとし、ある正の整数...
...�まる。 これにより、$V$\ を $k[X]$-加群と見よう。
\end{itembox}](img1.png)
![$ k[X]$](img2.png) は PID であるから、一般論(命題10.7)により、
次の命題が成り立つことがわかる。
は PID であるから、一般論(命題10.7)により、
次の命題が成り立つことがわかる。
命題 11.1
基本仮定のもとで、
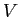
は
![$ k[X]/(p(X)^e) $](img4.png)
(
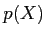
は
![$ k[X]$](img2.png)
の素元。
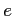
は正の整数) の形の
![$ k[X]$](img2.png)
-加群の直和である。
命題 11.2
![$ f(X)\in k[X]$](img7.png)
を
と書こう。
![$ g(X)\in k[X]$](img9.png)
の
![$ k[X]/(f(X))$](img10.png)
におけるクラスを
![$ [g]_f$](img11.png)
と書くことにする。
このとき、
-
![$ k[X]/(f(X))$](img10.png) の基底として、
の基底として、
が取れる。
- 上の基底を用いると
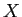 の作用は
の作用は
と書き下せる。
例 11.3
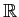
![$ [X]/(X^2+1)$](img16.png)
の基底として
![$ b_0=[1]_{X^2+1}, b_1=[X]_{X^2+1}$](img17.png)
が取れる。
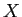
のこの基底への作用は、
で与えられる。行列で表現すれば、
という具合である。
定義 11.4
体
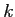
が
代数的閉体であるとは、
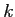
上の任意の(次数が
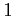
以上の)
一変数多項式
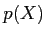
が
一次式の積に分解するときに言う。
複素数体
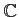 は代数的閉体であることが知られている。任意の体
は代数的閉体であることが知られている。任意の体 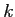 に対して、
それを含むような最小の代数的閉体
に対して、
それを含むような最小の代数的閉体 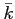 が存在することが
知られている。このような
が存在することが
知られている。このような 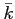 のことを
のことを 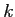 の代数的閉包
と呼ぶ。
の代数的閉包
と呼ぶ。
以下、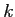 が代数的閉体のときを主に考える。このときには
が代数的閉体のときを主に考える。このときには 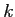 上の一変数
既約多項式は一次式に限るから、次のことがわかる。
上の一変数
既約多項式は一次式に限るから、次のことがわかる。
命題 11.5
基本仮定のもとで、さらに
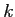
が代数的閉体であるとき、
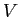
は
![$ k[X]/((X-c)^e)$](img25.png)
(
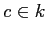
,
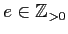
) の形の
![$ k[X]$](img2.png)
-加群と同型である。
命題11.2のような基底を取れば、
![$ k[X]/(X-c)^e$](img28.png) 上の
上の
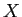 の作用の表現を得ることができるが、
の作用の表現を得ることができるが、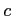 だけずらすことによって、
さらに良い基底を取ることもできる。
だけずらすことによって、
さらに良い基底を取ることもできる。
命題 11.6
-
![$ k[X]/((X-c)^e)$](img25.png) の基底として、
の基底として、
が取れる。
- 上の基底を用いると
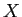 の作用は
の作用は
と書き下せる。行列で書くと
もしくは、基底の順番を取り換えて、
ただし
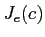 はジョルダン細胞と呼ばれる次のような行列である。
はジョルダン細胞と呼ばれる次のような行列である。
系 11.7
代数的閉体
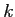
上の行列
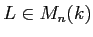
が与えられたとき、
うまい基底変換行列
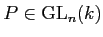
をとれば、
とジョルダン細胞の「直和」に分解される。
問題 11.1
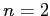
で、
のとき、基本仮定のようにして
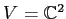
を
![$ {\mathbb{C}}[X]$](img42.png)
加群と見よう。
このとき、
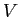
は
![$ k[X]$](img2.png)
上
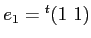
で生成されることを示しなさい。
問題 11.2
前問の仮定のもとで、
![$ {\mathbb{C}}[X]$](img42.png)
-加群の同型
![$ {\mathbb{C}}[X]/(X-2)(X-3) \cong V$](img44.png)
を作ってみせなさい。



Next: About this document ...
2013-06-24
![\begin{itembox}[l]{基本仮定}
$k$\ は体であるとし、ある正の整数...
...�まる。 これにより、$V$\ を $k[X]$-加群と見よう。
\end{itembox}](img1.png)
![\begin{itembox}[l]{基本仮定}
$k$\ は体であるとし、ある正の整数...
...�まる。 これにより、$V$\ を $k[X]$-加群と見よう。
\end{itembox}](img1.png)
![]() は PID であるから、一般論(命題10.7)により、
次の命題が成り立つことがわかる。
は PID であるから、一般論(命題10.7)により、
次の命題が成り立つことがわかる。
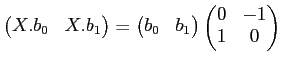
![]() は代数的閉体であることが知られている。任意の体
は代数的閉体であることが知られている。任意の体 ![]() に対して、
それを含むような最小の代数的閉体
に対して、
それを含むような最小の代数的閉体 ![]() が存在することが
知られている。このような
が存在することが
知られている。このような ![]() のことを
のことを ![]() の代数的閉包
と呼ぶ。
の代数的閉包
と呼ぶ。
![]() が代数的閉体のときを主に考える。このときには
が代数的閉体のときを主に考える。このときには ![]() 上の一変数
既約多項式は一次式に限るから、次のことがわかる。
上の一変数
既約多項式は一次式に限るから、次のことがわかる。
![]() 上の
上の
![]() の作用の表現を得ることができるが、
の作用の表現を得ることができるが、![]() だけずらすことによって、
さらに良い基底を取ることもできる。
だけずらすことによって、
さらに良い基底を取ることもできる。