第6回目の主題 :
![]()
次のことをこの講義からしばらくの間の目標にしよう。
言葉の確認から:
可換環 ![]() は、0
以外に零因子を持たないとき整域と呼ばれるのでした。
は、0
以外に零因子を持たないとき整域と呼ばれるのでした。
「余りを許した割り算」が必ずできるような整域のことを ユークリッド整域と呼ぶのでした。
次の定理は代数IB で学習済みのことと思います。
これらの諸定理から、次のことがすぐに分かる。
なる関係式が成り立っていたとする。このとき、
次のような
![]() が存在する。
が存在する。
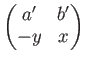
は
は必ず有限で止まる。すなわち、ある
が成り立つ。