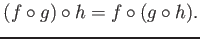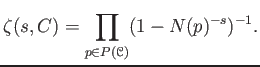- A collection
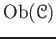 of objects of
of objects of
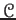 .
.
- For each pair of objects
 , a set
, a set
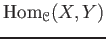
of morphisms. - For each triple of objects
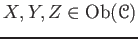 ,
a map(``composition (rule)'')
,
a map(``composition (rule)'')
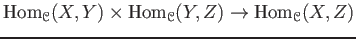
satisfying the following axioms
-
 unless
unless
 .
.
- (Existence of an identity) For any
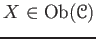 ,
there exists an element
,
there exists an element
 such that
such that
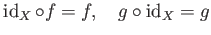
holds for any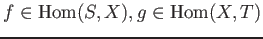 (
(
 ).
).
- (Associativity)
For any objects
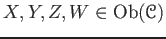 , and for any morphisms
, and for any morphisms
 ,
we have
,
we have