![]()
行列式
二次行列の場合
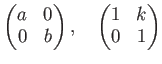
によって面積がそれぞれ
単位正方形の面積が線形変換 ![]() で何倍になるかを表すのが、
で何倍になるかを表すのが、![]() の
行列式 (
の
行列式 (
![]() ) である。ただし、
) である。ただし、![]() によって向きが変わるか否かによって
によって向きが変わるか否かによって
![]() には符号がつく。
定義から、
には符号がつく。
定義から、
が成り立つ。
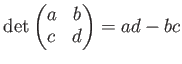
と与えられる。
3次以上の行列についても、その行列式が同様に定義される。
置換 ![]() には置換行列
には置換行列
![]() がつきものであった。その行列式を
がつきものであった。その行列式を
![]() の符号とよび、
の符号とよび、
![]() で表す。
で表す。
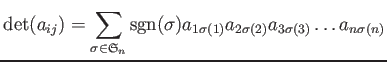
&dotfill#dotfill;
置換についての補遺。
置換
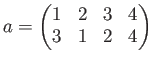
は、
というようにも書く。
二つの置換の結合(演算)は通常《後ろから読》む。たとえば、
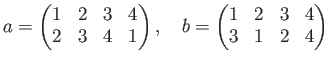
の掛け算
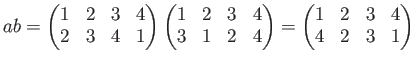
つまり、例えば
いくつかの元
![]() を順繰りに変える置換、すなわち
を順繰りに変える置換、すなわち
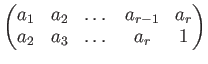
のことを (長さ
長さ ![]() の巡回置換のことを互換と呼ぶ。例えば、
の巡回置換のことを互換と呼ぶ。例えば、![]() は,
は,
![]() と
と ![]() とを入れ換える置換である。
とを入れ換える置換である。