行列に基本行列を左右から(ごちゃ混ぜに)掛けることにより、行列を
![]() と書く行列
(
と書く行列
(![]() 成分がはじめの
成分がはじめの ![]() 個だけ
個だけ ![]() であとはすべて 0
.)
に変形できるのでした。
であとはすべて 0
.)
に変形できるのでした。
&dotfill#dotfill;
![]() 行列の階数(ランク)
行列の階数(ランク)
任意の ![]() 行列
行列 ![]() は、うまく両側基本変形すれば、
両側基本変形の標準形の行列に変形できるのでした。それを利用すると
行列のランクが定義されます。
は、うまく両側基本変形すれば、
両側基本変形の標準形の行列に変形できるのでした。それを利用すると
行列のランクが定義されます。
証明には次の補題を用いる。
命題10.2により、次のことがすぐにわかる。
◎階数と正則性
◎階数の幾何学的な意味
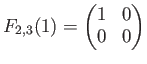 について調べよう。
この行列は
について調べよう。
この行列は
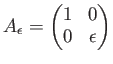 の
の
![]() の
「極限」 と考えられる。
行列
の
「極限」 と考えられる。
行列
![]() は,「縦に
は,「縦に ![]() 倍、横には等倍」という行列である。
の
倍、横には等倍」という行列である。
の
![]() の
「極限」 では、この写像は縦方向を完全に潰す。
つまり、
の
「極限」 では、この写像は縦方向を完全に潰す。
つまり、
![]() は縦方向を完全に潰す写像である。(論理的には、基本ベクトルの
行き先を見たほうがよいが、結論は同じである。)
は縦方向を完全に潰す写像である。(論理的には、基本ベクトルの
行き先を見たほうがよいが、結論は同じである。)
同様に、
![]() は、
は、
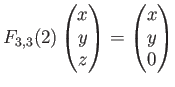
という線形写像をあたえる。この行列は
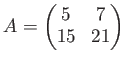
について、
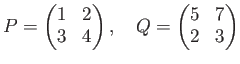
と置くと、
という分解が成り立つ。
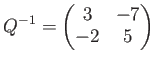
であって、
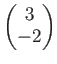 を
を 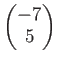 を
を
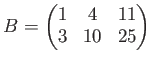
について、
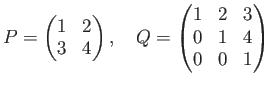
と置くと、
という分解が成り立つ。
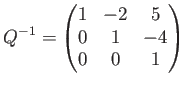
であって、
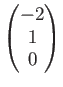 を
を 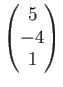 を
を
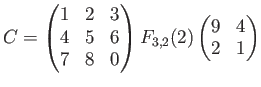
と、
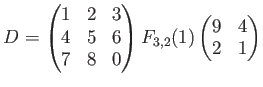
について、それぞれの分解に即して どのベクトルをどのベクトルに送る写像か上の例のように述べよ。