è،Œهˆ—مپ«هں؛وœ¬è،Œهˆ—م‚’هڈ³مپ‹م‚‰وژ›مپ‘م‚‹مپ“مپ¨مپ«م‚ˆم‚ٹم€پè،Œهˆ—م‚’ ه¤‰ه½¢مپ§مپچم‚‹مپ®مپ§مپ—مپںم€‚ هڈ³هں؛وœ¬ه¤‰ه½¢م‚’駆ن½؟مپ™م‚‹مپ“مپ¨مپ§م€پè،Œهˆ—مپ®é€†è،Œهˆ—م‚’計算مپ§مپچمپ¾مپ™م€‚
&dotfill#dotfill;
![]() è،Œهˆ—مپ®هں؛وœ¬ه¤‰ه½¢
è،Œهˆ—مپ®هں؛وœ¬ه¤‰ه½¢
â—ژهڈ³هں؛وœ¬ه¤‰ه½¢
ن¸ژمپˆم‚‰م‚Œمپںè،Œهˆ— ![]() (و£و–¹è،Œهˆ—مپ¨é™گم‚‰مپھمپ„) مپ«مپںمپ„مپ—م€پ
هں؛وœ¬è،Œهˆ—(مپ“م‚Œمپ¯و£و–¹è،Œهˆ—)م‚’هڈ³مپ‹م‚‰مپ„مپڈمپ¤مپ‹مپ‹مپ‘م‚‹مپ“مپ¨مپ«م‚ˆم‚ٹم€پ
(و£و–¹è،Œهˆ—مپ¨é™گم‚‰مپھمپ„) مپ«مپںمپ„مپ—م€پ
هں؛وœ¬è،Œهˆ—(مپ“م‚Œمپ¯و£و–¹è،Œهˆ—)م‚’هڈ³مپ‹م‚‰مپ„مپڈمپ¤مپ‹مپ‹مپ‘م‚‹مپ“مپ¨مپ«م‚ˆم‚ٹم€پ![]() مپ¨هگŒمپکم‚µم‚¤م‚؛مپ®و–°مپ—مپ„è،Œهˆ—م‚’ن½œم‚‹مپ“مپ¨مپŒمپ§مپچم‚‹م€‚
مپ“مپ®و“چن½œم‚’هڈ³هں؛وœ¬ه¤‰ه½¢مپ¨مپ„مپ†م€‚
مپ¨هگŒمپکم‚µم‚¤م‚؛مپ®و–°مپ—مپ„è،Œهˆ—م‚’ن½œم‚‹مپ“مپ¨مپŒمپ§مپچم‚‹م€‚
مپ“مپ®و“چن½œم‚’هڈ³هں؛وœ¬ه¤‰ه½¢مپ¨مپ„مپ†م€‚
هڈ³هں؛وœ¬ه¤‰ه½¢مپ¯م€پهں؛وœ¬مƒ™م‚¯مƒˆمƒ«مپ®è،Œمپچه…ˆم‚’مپ؟م‚‹مپ“مپ¨مپ§çگ†è§£مپ™م‚‹مپ“مپ¨مپŒمپ§مپچم‚‹م€‚
مپ¨مپ„مپ†م‚ڈمپ‘مپ§م€پمپ“م‚Œم‚‰م‚’هˆ—هں؛وœ¬ه¤‰ه½¢مپ¨م‚‚言مپ†م€‚
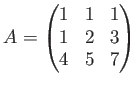
مپ«هں؛وœ¬ه¤‰ه½¢م‚’ç¹°م‚ٹè؟”مپ—مپ¦
ن¸ٹمپ®ه‘½é،Œ 9.1مپ¨هگŒو§کمپ«م€پ و¬،مپ®ه‘½é،Œم‚’証وکژمپ™م‚‹مپ“مپ¨مپŒمپ§مپچم‚‹م€‚
(مپ“م‚Œم‚‰م‚’è،Œهں؛وœ¬ه¤‰ه½¢مپ¨مپ„مپ†م€‚)
![]() مپ¨مپ„مپ†مپ“مپ¨مپ¯è¦ڑمپˆمپ¦مپٹمپڈمپ¨è‰¯مپ„م€‚
مپ¨مپ„مپ†مپ“مپ¨مپ¯è¦ڑمپˆمپ¦مپٹمپڈمپ¨è‰¯مپ„م€‚
ه·¦م€پهڈ³هں؛وœ¬ه¤‰ه½¢م‚’ç¹°م‚ٹè؟”مپ™مپ“مپ¨مپ«م‚ˆم‚ٹم€پè،Œهˆ—م‚’م‚ˆم‚ٹç°،هچکمپھه½¢مپ«مپ—مپںمپ„م€‚ مپ¤مپژمپ®و–¹é‡مپŒè€ƒمپˆم‚‰م‚Œم‚‹م€‚
مپ©مپ®و–¹é‡م‚’مپ¨مپ£مپ¦مپ„م‚‹مپ‹م‚’و„ڈèکمپ™م‚‹مپ“مپ¨مپŒه¤§ن؛‹مپ§مپ‚م‚‹م€‚
ه‰چه›مپ¯م€پ(و–¹é‡1)مپ§è€ƒمپˆمپںمپ®مپ§مپ‚مپ£مپںم€‚ (و–¹é‡2)مپ¯(و–¹é‡1)مپ¨ن¼¼مپںم‚ˆمپ†مپھمپ“مپ¨مپ«مپھم‚‹م€‚ ن»ٹه›مپ¯م€پ(و–¹é‡3)مپ§è€ƒمپˆمپ¦مپ؟م‚ˆمپ†م€‚
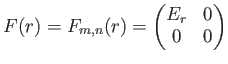
م‚’م€پن¸،هپ´هں؛وœ¬ه¤‰ه½¢مپ®و¨™و؛–ه½¢مپ®è،Œهˆ—مپ¨ه‘¼مپ¶م€‚
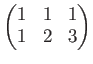
م‚’ن¸،هپ´هں؛وœ¬ه¤‰ه½¢مپ—م€پو¨™و؛–ه½¢مپ«ç›´مپ—مپھمپ•مپ„م€‚
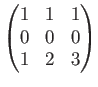
م‚’ن¸،هپ´هں؛وœ¬ه¤‰ه½¢مپ—م€پو¨™و؛–ه½¢مپ«ç›´مپ—مپھمپ•مپ„م€‚
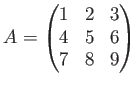
م‚’ن¸،هپ´هں؛وœ¬ه¤‰ه½¢مپ—م€پو¨™و؛–ه½¢مپ«ç›´مپ—مپھمپ•مپ„م€‚