![]() ベクトルの一次独立性(続)。一次写像。
ベクトルの一次独立性(続)。一次写像。
ベクトル
![]()
![]()
![]()
![]()
![]()
![]() は、
その自明でない線形結合
は、
その自明でない線形結合
が 0 に等しくなりうるとき、線形従属、 そうでないとき、線形独立であるというのでした。 線形独立性は、和とスカラー倍という線形代数らしい 言葉で語ることができる一方、それは成分で書くと連立一次方程式と 関連しているのでした。
&dotfill#dotfill;
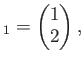
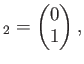
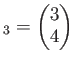
とおくと、
だからである。
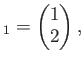
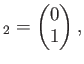
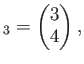
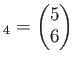
とおくと、
だからである。(一般に、一次従属なベクトルのあつまりに余分なベクトルを 付け加えてもやはり一次従属である。)
上の例で、
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() の
あいだの線形関係をカンに頼らずに求めるには、連立方程式
の
あいだの線形関係をカンに頼らずに求めるには、連立方程式
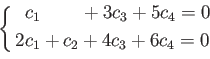
を解けば良い。
想像がつくように、二次元ベクトル空間 ![]() の 3個以上のベクトルは必ず
一次従属である。このことは、一般のベクトル空間の「次元」を一次独立性を
用いて定義できる可能性を示している。
実は、ベクトル空間
の 3個以上のベクトルは必ず
一次従属である。このことは、一般のベクトル空間の「次元」を一次独立性を
用いて定義できる可能性を示している。
実は、ベクトル空間 ![]() が与えられた時、その中で一次独立なベクトルの
最大数のことを
が与えられた時、その中で一次独立なベクトルの
最大数のことを ![]() の次元というのである。
の次元というのである。
&dotfill#dotfill;
数ベクトル空間
![]()
![]() と、ほかのベクトル空間を比べたくなる。
あるいは、ベクトル空間同士を比べることもあるだろう。
そのために、次のようなものを使う。
と、ほかのベクトル空間を比べたくなる。
あるいは、ベクトル空間同士を比べることもあるだろう。
そのために、次のようなものを使う。
「線形」という言葉の由来は次の命題から分かるかもしれない。
なる形をしたものである。
なる形をしたものである。
この定義では「直線」や「線分」として
![]()
![]()
![]()
![]() の場合
(本来は「点」と呼ぶべきもの)を含む。そのほうが下の命題の記述が
簡潔になってラクだからだが、使用の場合にはちょっと注意が必要である。
の場合
(本来は「点」と呼ぶべきもの)を含む。そのほうが下の命題の記述が
簡潔になってラクだからだが、使用の場合にはちょっと注意が必要である。
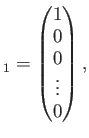
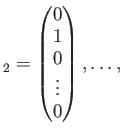
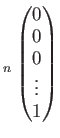
(
※レポート問題
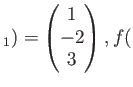
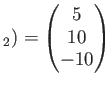
を満足するとする。このとき
を満たすとするとき、上の図形を