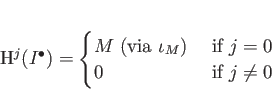Next: Bibliography
Commutative algebra
Yoshifumi Tsuchimoto

DEFINITION 08.1
Let

be a ring.
A
cochain complex of

-modules
is a sequence of

-modules
such that
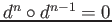
.
The
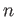
-th
cohomology of the cochain complex is defined to be the

-module
Elements of
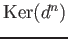
(respectively,
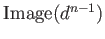
)
are often referred to as
cocycles (respectively,
coboundaries).
EXERCISE 08.1
Let

be a ring. Let
be an exact sequence of

-modules.
Assume furthermore that
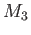
is projective.
Then show that
the sequence
is exact.
LEMMA 08.3
Let  be a (unital associative but not necessarily commutative) ring.
Then for any
be a (unital associative but not necessarily commutative) ring.
Then for any  -module
-module 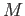 , the following conditions are equivalent.
, the following conditions are equivalent.
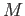 is a direct summand of free modules.
is a direct summand of free modules.
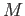 is projective
is projective
COROLLARY 08.4
For any ring  , the category
, the category
 of
of  -modules
have enough projectives. That means, for any object
-modules
have enough projectives. That means, for any object
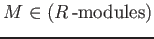 ,
there exists a projective object
,
there exists a projective object 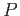 and a surjective morphism
and a surjective morphism
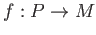 .
.
DEFINITION 08.5
Let

be a commutative ring.
We assume

is a domain (that means,

has no zero-divisors except for 0
.)
An  -module
-module 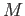 is said to be divisible if
for any
is said to be divisible if
for any
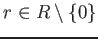 , the multplication map
, the multplication map
is surjective.
DEFINITION 08.6
Let

be a commutative ring.
We assume

is a domain (that means,

has no zero-divisors except for 0
.)
An  -module
-module 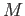 is said to be divisible if
for any
is said to be divisible if
for any
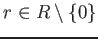 , the multplication map
, the multplication map
is epic.
LEMMA 08.7
Let  be a (commutative) principal ideal domain (PID).
Then an
be a (commutative) principal ideal domain (PID).
Then an  -module
-module 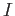 is injective if and only if it is divisible.
is injective if and only if it is divisible.
A bit of category theory:
DEFINITION 08.9
A
category
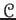
is a collection of the following data
- A collection
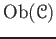 of objects of
of objects of
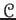 .
.
- For each pair of objects
 , a set
, a set
of morphisms.
- For each triple of objects
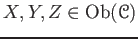 ,
a map(``composition (rule)'')
,
a map(``composition (rule)'')
satisfying the following axioms
-
 unless
unless
 .
.
- (Existence of an identity) For any
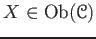 ,
there exists an element
,
there exists an element
 such that
such that
holds for any
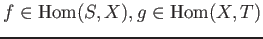 (
(
 ).
).
- (Associativity)
For any objects
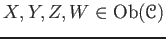 , and for any morphisms
, and for any morphisms
 ,
we have
,
we have
Morphisms are the basic actor/actoress in category theory.
An additive category is a category in which one may ``add'' some morphisms.
DEFINITION 08.10
An additive category
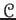
is said to be
abelian if it satisfies the
following axioms.
- A4-1.
- Every morphism
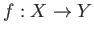 in
in
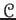 has a kernel
has a kernel
 .
.
- A4-2.
- Every morphism
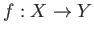 in
in
 has a
cokernel
has a
cokernel
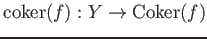 .
.
- A4-3.
- For any given morphism
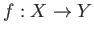 , we have
a suitably defined isomorphism
, we have
a suitably defined isomorphism
in
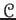 .
More precisely,
.
More precisely, 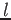 is a morphism which is defined by the following relations:
is a morphism which is defined by the following relations:
By employing the following axiom
instead of the axiom (functor-2) above, we obtain a definition of
a contravariant functor:
(functor-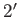 )
)
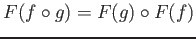 for any composable morphisms
for any composable morphisms
DEFINITION 08.12
Let
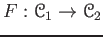
be a functor between additive categories.
We call
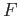 additive
additive if for any objects
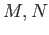
in
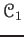
,
is additive.
DEFINITION 08.13
Let
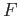
be an additive functor from an abelian category
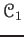
to
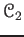
.
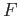 is said to be left exact (respectively, right exact )
if for any exact sequence
is said to be left exact (respectively, right exact )
if for any exact sequence
the corresponding map
(respectively,
is exact
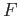 is said to be exact if it is both left exact and right exact.
is said to be exact if it is both left exact and right exact.
LEMMA 08.14
Let  be a (unital associative but not necessarily commutative) ring.
Then for any
be a (unital associative but not necessarily commutative) ring.
Then for any  -module
-module 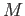 , the following conditions are equivalent.
, the following conditions are equivalent.
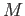 is a direct summand of free modules.
is a direct summand of free modules.
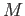 is projective
is projective
COROLLARY 08.15
For any ring  , the category
, the category
 of
of  -modules
have enough projectives. That means, for any object
-modules
have enough projectives. That means, for any object
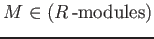 ,
there exists a projective object
,
there exists a projective object 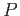 and a surjective morphism
and a surjective morphism
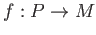 .
.
DEFINITION 08.16
Let

be a commutative ring.
We assume

is a domain (that means,

has no zero-divisors except for 0
.)
An  -module
-module 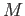 is said to be divisible if
for any
is said to be divisible if
for any
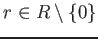 , the multplication map
, the multplication map
is surjective.
DEFINITION 08.17
Let

be a commutative ring.
We assume

is a domain (that means,

has no zero-divisors except for 0
.)
An  -module
-module 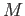 is said to be divisible if
for any
is said to be divisible if
for any
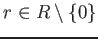 , the multplication map
, the multplication map
is epic.
DEFINITION 08.18
Let
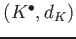
,
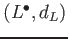
be complexes of objects
of an additive category
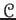
.
- A morphism of complex
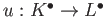 is a family
is a family
of morphisms in
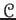 such that
such that 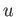 commutes with
commutes with 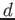 . That means,
. That means,
holds.
- A homotopy between two morphisms
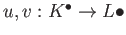 of complexes is a family of morphisms
of complexes is a family of morphisms
such that
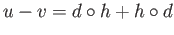 holds.
holds.
DEFINITION 08.20
Let
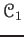
be an abelian category which has enough injectives.
Let
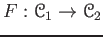
be a left exact functor to an abelian category.
Then for any object
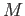
of
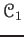
we take an injective resolution
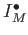
of
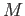
and define
and call it the derived functor of
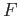
.
LEMMA 08.21
The derived functor is indeed a functor.



Next: Bibliography
2012-06-28
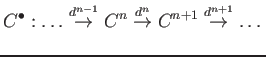
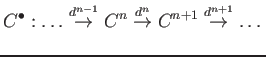
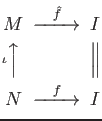
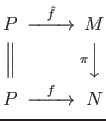
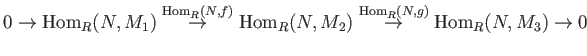
![]() -module
-module ![]() is said to be divisible if
for any
is said to be divisible if
for any
![]() , the multplication map
, the multplication map
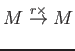
![]() -module
-module ![]() is said to be divisible if
for any
is said to be divisible if
for any
![]() , the multplication map
, the multplication map
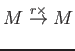
![]() )
)
![]() for any composable morphisms
for any composable morphisms
![]() -module
-module ![]() is said to be divisible if
for any
is said to be divisible if
for any
![]() , the multplication map
, the multplication map
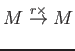
![]() -module
-module ![]() is said to be divisible if
for any
is said to be divisible if
for any
![]() , the multplication map
, the multplication map