be an exact sequence of
Yoshifumi Tsuchimoto
be an exact sequence of
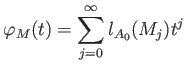
![$\displaystyle \prod_{j=1}^r (1-t^{d_j}) \varphi_M(t) \in \mathbb{Q}[t]
$](img14.png)
We call
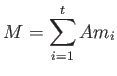
holds. If an ideal
then there exists an element
holds. If furthermore
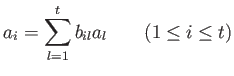
holds. In a matrix notation, this may be rewritten as
with
Now let
Then we have
On the other hand, since
![]()