


Next: About this document ...
Commutative algebra
Yoshifumi Tsuchimoto

Recall that for any commutative ring 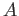 ,
we define its (Krull) dimension
,
we define its (Krull) dimension  as
the Krull dimension of
as
the Krull dimension of
 .
.
DEFINITION 04.1
Let
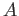
be a commutative ring.
For any
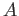
-module
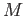
, we define its dimension as
where
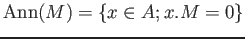
.
DEFINITION 04.2
For any
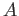
-module
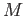
of a ring
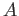
, we define its length
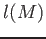
as the
supremum of the lenths of descending chains of submodules of
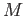
.
EXAMPLE 04.3
Let
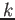
be a commutative field. A
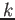
-module
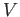
is a vector space over
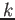
.
The lengh of
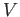
is then equal to the dimension of
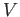
as a
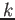
-vector space.
In what follows, we denote it as
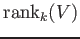
.
EXERCISE 04.1
Compute the lenth of a
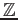
-module

.
DEFINITION 04.4
Let
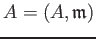
be a local ring. Let
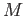
be an
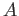
-module.
we define

to be the smallest value of
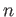
such that there exist
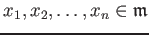
for which
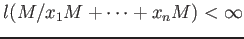
.
Let us recall the definition of Noetherian ring.
DEFINITION 04.5
A ring is called
Noetherian if any
asscending chain
stops after a finite number of steps. (That means, There exists a number
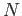
such that
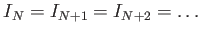
.)
PROPOSITION 04.6
A commutative ring  is Noetherina if and only if
its ideals are always finitely generated.
is Noetherina if and only if
its ideals are always finitely generated.
DEFINITION 04.7
Let
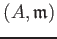
be a be a Noetherian local ring. Let
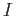
be
an ideal of
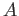
. We say that
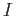
is an ideal of definition if
there exists an integer
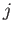
such that
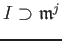
.
Then for any finite
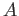
-module
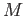
, we define
It is known that there exists a polynomal
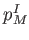
such that
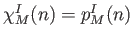
for

. We define
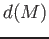
as the
degree of the polynomial
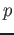
.
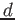
does not depend on the choice of the ideal
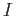
of definition.
PROPOSITION 04.8
For any Noetherian local ring 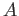 and for any finite
and for any finite 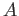 -module
-module 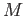 , we have
, we have
DEFINITION 04.9
For any local ring
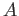
, we define its embedding dimension as
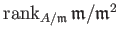
.
DEFINITION 04.10
A Noetherian local ring is said to be regular if its embedding dimension
is equal to the dimension of
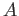
.



Next: About this document ...
2012-05-11
![]() ,
we define its (Krull) dimension
,
we define its (Krull) dimension ![]() as
the Krull dimension of
as
the Krull dimension of
![]() .
.