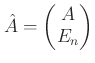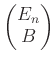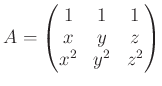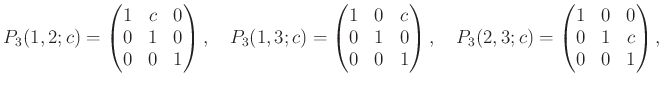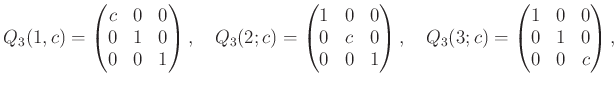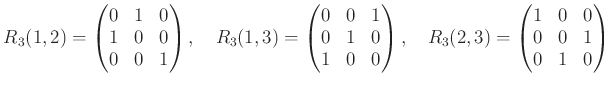Next: About this document ...
線形代数学概論 A No.8要約
行列 は
普通の数のように、足したり引いたり掛けたりできるのでした。
行列をブロックに区分けすることにより、計算を簡単にすることができる
場合がありました。
&dotfill#dotfill;
 行列の基本変形
行列の基本変形
- この定義の記号は(教科書とは合わせてあるが)、ここだけのものである。
- 上の定義で「列」を「行」に変えても全く同じ行列を得る。
- スペースの関係で、例は一番最後にあげる。"..." を用いた一般の場合の
書き方については、講義か、教科書を参照のこと。
◎ 置換と置換行列
上の 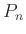 は「シフト」の一般化。
は「シフト」の一般化。 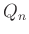 は 対角行列である。
は 対角行列である。
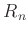 については新しく出てきた。これは「置換行列」と見るのが自然である。
これを説明しよう。
については新しく出てきた。これは「置換行列」と見るのが自然である。
これを説明しよう。
定義 8.2
一般に、
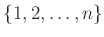
の順番を並べ替えたものを
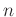
個の元の
置換という。
これは
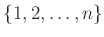
からそれ自身への全単射
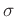
をあたえて、
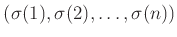
という並びを
考えるというのと同じ事である。そこで、以下では置換と言えばそのような
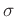
のことであると考えることにする。
定義 8.3
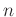
個の元の置換
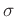
にたいし、
なる行列のことを
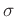
に対応する
置換行列と呼ぶ。
定義 8.4
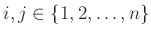
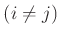
に対し、
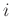
と
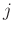
を入れ替えるような
置換のことを(
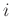
と
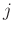
の)
互換 とよび、
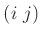
で書き表す。
すなわち、
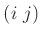
とは、次のような置換
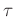
のことである。
置換行列の言葉を用いれば、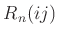 は互換
は互換 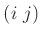 に対応する置換行列と
言うことになる。
に対応する置換行列と
言うことになる。
◎右基本変形
与えられた行列 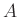 (正方行列と限らない) にたいし、
基本行列(これは正方行列)を右からいくつかかけることにより、
(正方行列と限らない) にたいし、
基本行列(これは正方行列)を右からいくつかかけることにより、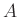 と同じサイズの新しい行列を作ることができる。
この操作を右基本変形という。
と同じサイズの新しい行列を作ることができる。
この操作を右基本変形という。
右基本変形は、基本ベクトルの行き先をみることで理解することができる。
次のことも基本的である。
命題 8.2
基本変形は可逆な操作である。
それに呼応して、基本行列は可逆な行列である。
「大抵の」正方行列 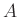 は右基本変形を連続して行うことにより単位行列
は右基本変形を連続して行うことにより単位行列 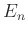 に
変形できる。つまり、基本行列
に
変形できる。つまり、基本行列
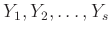 があって、
があって、
そこで
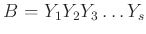 とおけば、
とおけば、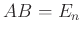 である。
である。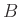 は逆行列を持つので、
は逆行列を持つので、
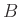 が
が 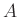 の逆行列であることがわかる。
つまり、
の逆行列であることがわかる。
つまり、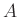 にどんな右基本変形をすれば
にどんな右基本変形をすれば 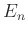 になるかを詳細に記録すれば、
になるかを詳細に記録すれば、
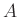 の逆行列が計算できる。右基本変形をいちいち記録しておくのは面倒である。
次のようなトリックを用いるとよい。
の逆行列が計算できる。右基本変形をいちいち記録しておくのは面倒である。
次のようなトリックを用いるとよい。
命題 8.3
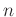 次正方行列
次正方行列 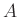 にたいして、それを
にたいして、それを 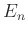 の上に積み上げた行列
の上に積み上げた行列
を考える。もし、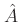 に右基本変形を繰り返して"上の部分"が
に右基本変形を繰り返して"上の部分"が 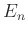 ,
すなわち
,
すなわち
のかたちとなったとすると、"下の部分"の 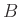 の部分が
の部分が 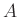 の逆行列である。
の逆行列である。
問題 8.1
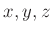
はどの2つも相異なるような実数とする。このとき、
に基本変形を繰り返して
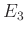
に変形せよ。(余力があれば、
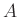
の逆行列をもとめよ。)
&dotfill#dotfill;
例 8.1 (
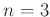
の基本行列)
| |
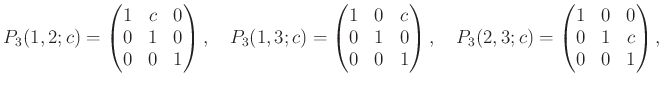 |
|
| |
他に成分が下半分にくるタイプももちろんあるが、 スペースの関係で省略する。 |
|
| |
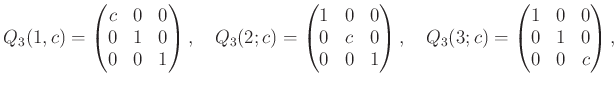 |
|
| |
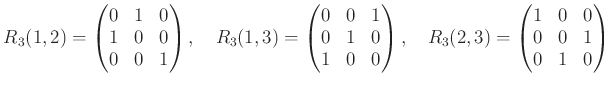 |
|



Next: About this document ...
2012-11-16
![]() 行列の基本変形
行列の基本変形
![]() は「シフト」の一般化。
は「シフト」の一般化。 ![]() は 対角行列である。
は 対角行列である。
![]() については新しく出てきた。これは「置換行列」と見るのが自然である。
これを説明しよう。
については新しく出てきた。これは「置換行列」と見るのが自然である。
これを説明しよう。
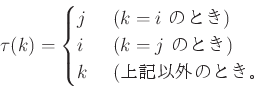
![]() は互換
は互換 ![]() に対応する置換行列と
言うことになる。
に対応する置換行列と
言うことになる。
![]() (正方行列と限らない) にたいし、
基本行列(これは正方行列)を右からいくつかかけることにより、
(正方行列と限らない) にたいし、
基本行列(これは正方行列)を右からいくつかかけることにより、![]() と同じサイズの新しい行列を作ることができる。
この操作を右基本変形という。
と同じサイズの新しい行列を作ることができる。
この操作を右基本変形という。
![]() は右基本変形を連続して行うことにより単位行列
は右基本変形を連続して行うことにより単位行列 ![]() に
変形できる。つまり、基本行列
に
変形できる。つまり、基本行列
![]() があって、
があって、