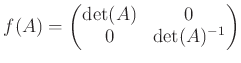Next: About this document ...
代数学 IA 演習問題 No.9
 《二つの群を比べるには、準同型を調べるのが基本である。》
《二つの群を比べるには、準同型を調べるのが基本である。》
準同型とは、演算を保つ写像の事である。
定義 9.1
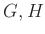
を群とする。
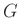
から
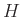
への写像
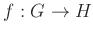
が準同型(正確には、群として
の準同型写像)であるとは、
任意の
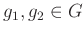
に対して、
が成り立つときに言う。 準同型
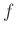
が全単射でもある時、
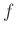
は同型であると言う。
問題 9.1
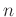
を正の整数とします。
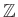
から
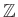
への写像
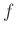
を、
で定めると、
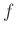
は準同型であることを示しなさい。
さらに、これは
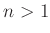
なら同型ではないことを示しなさい。。
問題 9.2
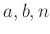
を正の整数とします。
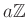
から
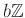
への写像
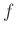
を、
で定めるとき、
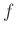
が準同型になるのは
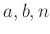
の間にどのような関係が
なりたつときか、答えなさい。
定義 9.2
以下では、《チャンネルの群》
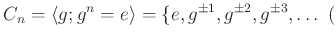
但し、$g^n=e$)
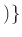
を頻繁に使います。この式は「
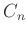
は一つの元
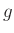
で生成された群で、
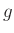
は
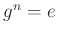
を基本関係式として持つ」と言う意味です。
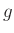
は「チャンネルを左に一目盛ひねる」と言う操作にあたります。
(アルファベットの 「
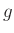
」にはとくに意味がありません。場合によっては
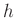
だとか、他の記号を使うこともあります。 )
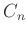
のことを、数学では、「位数
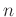
の巡回群」と言います。
問題 9.4 (0.5点)
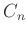
の位数を求めなさい。
問題 9.5
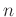
を正の整数とします。
から
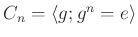
への写像を、
で定めると、
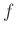
は準同型であることをしめしなさい。
さらに、これは同型ではないことを示しなさい。
問題 9.6
-
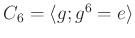 の元を全て書き出しなさい。
の元を全て書き出しなさい。
-
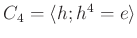 の元を全て書き出しなさい。
の元を全て書き出しなさい。
-
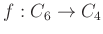 を
を
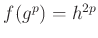 で定義します。
このとき、
で定義します。
このとき、 の各元は
の各元は  のどの元に対応するか、
上で書き出した元の間を矢印で結ぶことによって示しなさい。
のどの元に対応するか、
上で書き出した元の間を矢印で結ぶことによって示しなさい。
問題 9.7
-
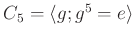 の元を全て書き出しなさい。
の元を全て書き出しなさい。
-
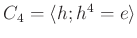 の元を全て書き出しなさい。
の元を全て書き出しなさい。
-
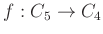 を
を
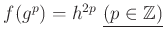 で定義しようとしても、
うまくいかない。
このことを、
で定義しようとしても、
うまくいかない。
このことを、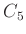 の各元は
の各元は 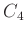 のどの元に対応するか、
上で書き出した元の間を矢印で結ぼうとすることによって示しなさい。
(
のどの元に対応するか、
上で書き出した元の間を矢印で結ぼうとすることによって示しなさい。
(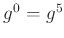 等に注意。)
等に注意。)
問題 9.8
を正の整数とします。
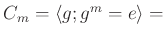
から
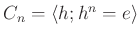
への写像を、
で定めようとします。このとき、
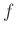
が準同型になるのはいつか、
答えなさい。
問題 9.9
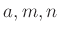
を正の整数とします。
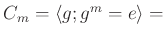
から
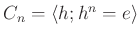
への写像を、
で定めようとします。このとき、
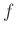
が準同型になるのはいつか、
答えなさい。
問題 9.10
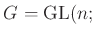
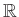
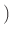
から、
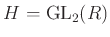
への写像
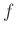
を、
で定義すると、
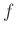
は準同型であることをしめしなさい。
定義 9.3
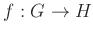
を二つの群の間の準同型とする。
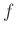
の核 (kernel) とは、
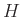
の単位元
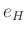
の
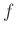
の逆像の事である。すなわち、
問題 9.11
問題
9.5 の写像
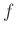
の核を求めなさい。
問題 9.12
問題
9.6 の写像
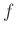
の核を求めなさい。
問題 9.13
群準同型
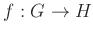
の核は一般に、
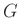
の正規部分群であることを
示しなさい。
問題 9.14
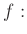
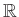
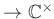
を、
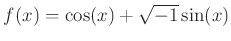
で定義すると、
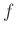
は群の準同型になることを示しなさい。さらに、
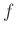
の核を求めなさい。
ただし、
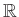
は実数全体の集合に足し算で演算を決めた群、
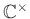
は
0
を除いた複素数にかけ算で演算を決めた群である。
問題 9.15
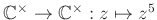
は群準同型であることを示し、
その核を元を全て書き表すことにより求めなさい。ただし、元は
(極座標表示)の形で表現すること。



Next: About this document ...
2012-06-11
![]() 《二つの群を比べるには、準同型を調べるのが基本である。》
《二つの群を比べるには、準同型を調べるのが基本である。》