


Next: About this document ...
1=4
代数学 演習IA問題 No.4
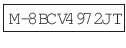
簡単な操作の例に、置換があります。「置き換え」ると言う意味を明確にするために、定義を確認しておきましょう。たとえば、元
は、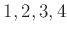 をならびかえて
をならびかえて 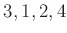 にすると言う意味ですが、そう覚えておくと後で混乱することがあるので、
にすると言う意味ですが、そう覚えておくと後で混乱することがあるので、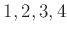 がそれぞれ《変身》して
がそれぞれ《変身》して 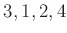 になると覚えておくのが良いと思います。
になると覚えておくのが良いと思います。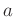 は《変身》と言う操作であって、これを、
は《変身》と言う操作であって、これを、
というようにも書きます。
ただし、違うものが同じものに変身してしまったり、あるものに変身するものがなかったりすると、《置き換え》になりませんから、それは除かなければなりません。
問題 4.1
無限個の元を持つ集合
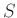
からそれ自身
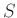
への写像では、一般に単射と全射は
同値ではありません。そこで整数全体の集合
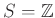
からそれ自身への写像
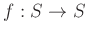
に対して、全射であるが、単射ではないもの例と、単射であるが、全射でないものの例を挙げなさい。
さて、二つの置換の結合(演算)は通常《後ろから読》みます。たとえば、
の掛け算 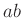 は、
は、
つまり、例えば 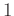 は
は 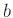 で
で 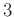 に化けて、次に
に化けて、次に 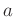 で
で 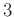 は
は 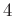 に化けるので、結果として
に化けるので、結果として 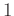 は
は 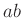 によって
によって 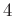 に化けることになります。
に化けることになります。
問題 4.2
上の 状況のもとで、
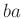
を求めなさい。
問題 4.3
を直接計算して示しなさい。
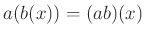
は置換一般について成り立ちます。
問題 4.4
三つの元
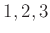
の置換をすべて求めなさい。(全部で
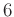
個あるはずです。)
任意の置換は互いに同じ文字を含まない巡回置換の積として表すことができます。例えば
、置換
をよくみてみると、次のような変身の様子が分かります。
したがって、
であることが分かります。
問題 4.6
次の各々の場合に
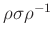
を求めなさい。
-
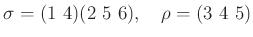
-
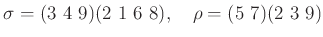
なお、答えは互いに同じ文字を含まない巡回置換の積として書いてみなさい。
(一般に、
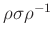 は
は 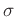 の
の 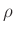 による共役元と呼ばれます
。)
による共役元と呼ばれます
。)
問題 4.7
置換の共役元の簡単な計算法を考えなさい。
問題 4.8
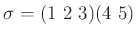
とします。
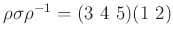
となる
ような
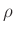
を一つ求めなさい。
定義 4.1
一般に、群
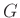
の元
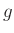
の位数とは、
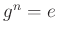
(単位元)となる最小の正の整数のことを
言います。また、群
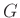
の位数と言うのは、
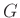
の元の数のことです。
問題 4.10
巡回置換
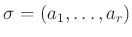
の位数を求めなさい。
問題 4.11 (各1)
-
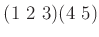 および
および
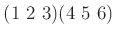 の位数を求めよ。
の位数を求めよ。
-
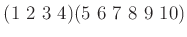 および
および
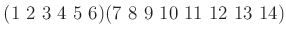 の位数を求めよ。
の位数を求めよ。
問題 4.12
二つの巡回置換
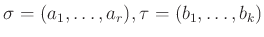
について、
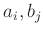
に同じ文字がないとき、積
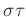
の位数を求めなさい。
定義 4.2
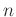
-個の元からなる集合
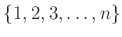
の上の置換の全体のなす群を
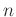
-次対称
群と呼び、
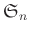
と書きます。
問題 4.13 (部分群一つにつき1点)
3次対称群
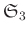
の部分群をすべて書きなさい。(全部で六つある筈です。)
問題 4.14
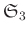
の部分群
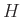
が、
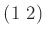
と
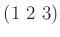
を含むとすると、
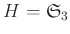
であることを示しなさい。
問題 4.15
4次対称群の元のそれぞれを、互いに同じ文字を含まない巡回置換の積として表しなさい
。(
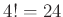
個あります!)
問題 4.16
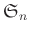
の部分群
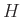
が、
互換
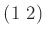
と巡回置換
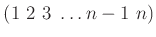
を含むとすると、
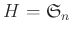
であることを証明しなさい。
問題 4.17
5つの元
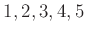
の置換はいくつあるか答えなさい。一般に
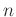
-個の元の置換の個数はいくつありますか?
問題 4.18
三つの元の置換のなす群
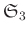
は正三角形の合同変換群
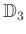
と
同型であること(群として同じであること)を示しなさい。
問題 4.19
4つの元の置換のなす群
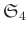
と正方形の合同変換群
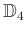
とは
同型でないことを示しなさい。
問題 4.20
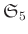
には位数
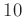
の元が存在しないことを示しなさい。



Next: About this document ...
2012-05-07
![]()
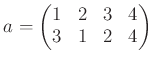
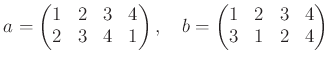
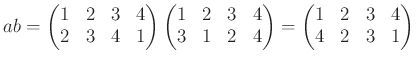
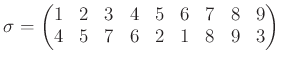
![]() は
は ![]() の
の ![]() による共役元と呼ばれます
。)
による共役元と呼ばれます
。)