


Next: About this document ...
代数学 IB No.12要約
 逆元といえば、ハイ互除法。
逆元といえば、ハイ互除法。
ユークリッド環(余りを許したわり算のできる環) 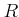 においては、
与えられた
においては、
与えられた 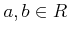 にたいし、
にたいし、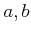 の最大公約数
の最大公約数 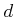 が存在し、
互除法により、
が存在し、
互除法により、
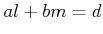 を満たす
を満たす 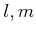 を具体的に求めることが
できるのでした。(No.8参照。)
を具体的に求めることが
できるのでした。(No.8参照。)
&dotfill#dotfill;
単項イデアル整域(PID) 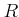 においては、与えられた
においては、与えられた 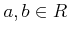 について、
命題 12.1 の二番目の条件を満たす
について、
命題 12.1 の二番目の条件を満たす
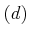 が存在することに注意。
が存在することに注意。
定理 12.2
PID 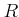 の元
の元 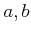 が互いに素であるとき、
が互いに素であるとき、
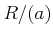 において、
において、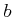 の同値類
の同値類 ![$ [b]_{(a)}$](img16.png) は逆元を
もつ。
は逆元を
もつ。
実際、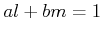 を満たす
を満たす 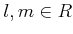 が存在する。
が存在する。![$ [l]_{(a)}$](img19.png) が
その逆元である。
が
その逆元である。
定義 12.1
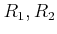
は環であるとする。このとき、
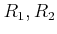
の環としての
直積
とは、デカルト積集合
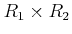
の上に、
次のような演算を定義したものである。
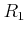
と
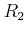
の環としての直積を、普通
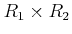
と書く。
補題 12.1
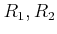 は環であるとする。このとき、
は環であるとする。このとき、
-
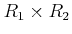 は環になる。
は環になる。
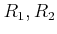 の単位元 がそれぞれ
の単位元 がそれぞれ
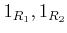 とすると、
とすると、
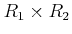 の単位元は
の単位元は
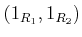 である。
である。
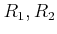 がともに可換ならば、
がともに可換ならば、
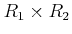 も可換である。
も可換である。
ベクトル空間で基本ベクトルが重要な役割を果たしたように、
環の直積においても、
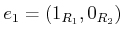 と
と
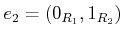 が
重要な役割を果たす。関係式
が
重要な役割を果たす。関係式
が成り立つことに注意せよ。
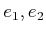 は直積の「射影」(もしくは射影元)と呼ばれる。
は直積の「射影」(もしくは射影元)と呼ばれる。
命題 12.3
環 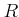 の元
の元 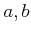 が
が 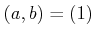 を満たすとき、
を満たすとき、
なる写像は環の同型を与える。
※三つの環
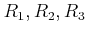 の直積も二つの場合と同様に定義される。
環
の直積も二つの場合と同様に定義される。
環
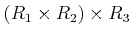 は
は
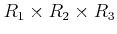 と
同型である。4つ以上でも同様。
と
同型である。4つ以上でも同様。
古典的な 105 減算は、
同型
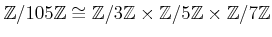 をもとにしている。
をもとにしている。
※レポート問題
つぎのうち一問を選択して解きなさい。
(期限:次の講義の終了時まで。)
- (I).
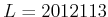 とおく。このとき、5桁以上の正の整数
とおく。このとき、5桁以上の正の整数 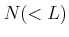 を自分できめて、その
を自分できめて、その 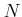 にたいして,
にたいして,
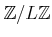 において、
において、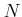 の逆元をもとめよ。
の逆元をもとめよ。
- (II).
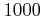 で割ると
で割ると 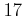 余り、
余り、 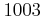 で割ると
で割ると 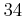 余るような整数
余るような整数 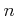 の例を一つ求めよ(途中の計算はある程度省略してよい。
ただし求めた方法は書いておくこと。)
の例を一つ求めよ(途中の計算はある程度省略してよい。
ただし求めた方法は書いておくこと。)



Next: About this document ...
2012-01-05
![]() 逆元といえば、ハイ互除法。
逆元といえば、ハイ互除法。
![]() においては、
与えられた
においては、
与えられた ![]() にたいし、
にたいし、![]() の最大公約数
の最大公約数 ![]() が存在し、
互除法により、
が存在し、
互除法により、
![]() を満たす
を満たす ![]() を具体的に求めることが
できるのでした。(No.8参照。)
を具体的に求めることが
できるのでした。(No.8参照。)
![]() と
と
![]() が
重要な役割を果たす。関係式
が
重要な役割を果たす。関係式
![]() の直積も二つの場合と同様に定義される。
環
の直積も二つの場合と同様に定義される。
環
![]() は
は
![]() と
同型である。4つ以上でも同様。
と
同型である。4つ以上でも同様。
![]() をもとにしている。
をもとにしている。