![]()
《割り算の原理(ユークリッド環)》 これ以降、この講義では「環」と単に言えば可換環のことを 指すことにする。
![]() と
と ![]() の二つにまず共通して言えることは、
どちらも「余りのある割り算」が出来ることである。
の二つにまず共通して言えることは、
どちらも「余りのある割り算」が出来ることである。
余りのある割り算なら出来るのが当たり前のことに思えるかも知れない。しかし、 たとえば
![]() の中で考えて
の中で考えて ![]() を
を ![]() で割った余りは?
で割った余りは?
![]() の中で考えて
の中で考えて ![]() を
を ![]() で割った余りは?
で割った余りは?
などと聞かれると困ってしまう。 ポイントは、 「どこで割り算が終ったか分かるような尺度があるかどうか」 という点にある。そこで次のような定義をする。
となる
割り算の原理としては次のこともよく使う。
となる
![]() の全てのイデアルが単項イデアルであるとき、
の全てのイデアルが単項イデアルであるとき、
![]() は単項イデアル環であると言う。
は単項イデアル環であると言う。
をみたす整数
をみたす
実際に ![]() を計算するには、次のような方法が便利である。
を計算するには、次のような方法が便利である。
を満たす整数
(解答) まず次のような計算を行う
| 小学生の計算(★) | 数式訳 | 行列算 |
| 72 わる 56 は 1 あまり 16 |
|
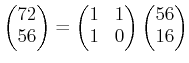
|
| 56 わる 16 は 3 あまり 8 |
|
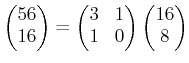
|
| 16 わる 8 は 2 あまり 0 |
|
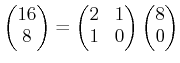
|
各々の行の行列算を組み合わせると、
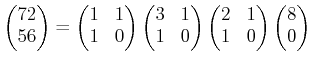
を得る。この式の右辺に現れる正方行列はすべて
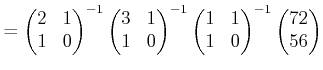 |
||
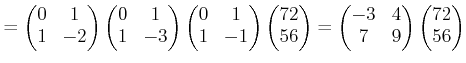 |
(答え)
![]() .
.
※レポート問題
つぎのうち一問を選択して解きなさい。 (期限:次の講義の終了時まで。)
を満たす多項式
の最大公約数をユークリッドの互除法を用いて求めなさい。
ヒント:
![]() であるから、まずは
であるから、まずは ![]() を
を ![]() で割ることになる。
で割ることになる。
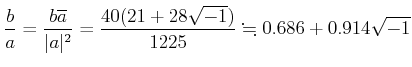
であるから、商
という具合になる。